Bei linearen Gleichungen handelt es sich um die einfachste Form von Gleichungen. Auf dieser Seite erfährst du vieles über lineare Gleichungen: Was sind überhaupt lineare Gleichungen und wie löst man sie? Wie kann man die Lösungen von linearen Gleichungen grafisch ermitteln? Zudem findest du auch zwei durchgerechnete Aufgaben.
Grundlegendes
Was versteht man unter linearen Gleichungen?
Lineare Gleichungen erkennt man daran, dass man sie so umformen kann, dass zuletzt nur mehr x in den Gleichungen stehen. Die höchste Potenz (=Hochzahl), die in einer linearen Gleichung vorkommt, ist also 1. Ein Beispiel für eine sehr einfache lineare Gleichung wäre:
$$4·x=12$$
Die Zahlen 4 und 12 nennt man Konstanten und das x ist die Variable. Variablen sind Platzhalter für Zahlen, die zunächst noch unbekannt sind. In der Regel verwendet man dafür die Kleinbuchstaben x und y, aber auch die Buchstaben a, b, c und d sind recht häufig in Gebrauch.
Wie löst man lineare Gleichungen?
Meist ist es das Ziel, die gegebene lineare Gleichung nach der gesuchten Variablen – das ist oft x – aufzulösen. Dazu muss man
- zunächst, falls vorhanden, alle Klammern von innen nach außen auflösen und
- danach alle x auf eine Seite der Gleichung bringen und alle Zahlen auf die andere Seite.
- Anschließend sind alle Terme mit x und alle Zahlen zusammenzurechnen.
- Zuletzt ist eventuell noch die Gleichung durch die Zahl, die vor dem x steht, zu dividieren.
Die sogenannte KLAPUSTRI-Regel ist stets zu beachten, das heißt: zuerst Klammern auflösen, dann Punktrechnungen und zuletzt Strichrechnugen durchführen. Etwas weiter unten auf der Seite findest du dazu natürlich auch ein Beispiel.
Wichtig ist zudem, stets auf beiden Seiten der Gleichung dasselbe tun. Man kann z. B. die gesamte Gleichung mit einer Zahl multiplizieren oder durch eine Zahl dividieren oder auch einzelne Terme auf beiden Seiten dazugeben oder wegnehmen.
Welche Lösungen kann es überhaupt geben?
In der Regel haben lineare Gleichungen jeweils genau eine Lösung, aber nicht alle Gleichungen haben eine Lösung und es gibt sogar lineare Gleichungen, für die alle Zahlen als Lösung infrage kommen. Im ersten Fall bekommt man als Ergebnis eine falsche Aussage, also zum Beispiel 3=9. Erhält man eine wahre Aussage, zum Beispiel 5=5, sind alle Zahlen Lösungen dieser Gleichung.
Grafische Darstellung der Lösung von linearen Gleichungen
Die Funktionsgleichung einer linearen Funktion lautet allgemein:
$$f(x)=k·x+d$$
Statt f(x) kann man auch y schreiben. Nullstellen werden berechnet, indem man f(x) gleich Null setzt. Daraus folgt:
$$0=k·x+d$$
In diese Form kann jede lineare Gleichung gebracht werden. Bei den Lösungen von linearen Gleichungen handelt es sich folglich um die Nullstellen von linearen Funktionen.
Probe
Setzt man die ermittelte Lösung in die ursprüngliche Gleichung ein, kann man prüfen, ob man richtig gerechnet hat. Man vergleicht dabei die linke Seite und die rechte Seite der Gleichung. Das nennt man Probe. Stimmt die Lösung, erhält man eine wahre Aussage, andernfalls eine falsche Aussage.
Durchgerechnete Beispiele
In diesem Abschnitt findest du zwei vollständig durchgerechnete Beispiele.
Beispiel 1: Sehr einfache lineare Gleichung
Das wäre ein Beispiel für eine sehr einfache lineare Gleichung:
$$4·x=12$$
Rechnerische Ermittlung der Lösung
Die Zahlen 4 und 12 sind die Konstanten und das x ist die Variable. Dividiert man nun beide Seiten der Gleichung durch 4, erhält man die Lösung:
$$4·x=12 \qquad /:4$$
$$\Rightarrow x=3$$
Grafische Ermittlung der Lösung
Dazu muss die Gleichung in die Form 0=k·x+d gebracht werden:
$$0=4·x-12$$
Es gibt zwei Funktionsgleichungen, wobei man y2 bekommt, indem man die obere Gleichung mit -1 multipliziert:
$$y_1=4·x-12$$
$$y_2=-4·x+12$$
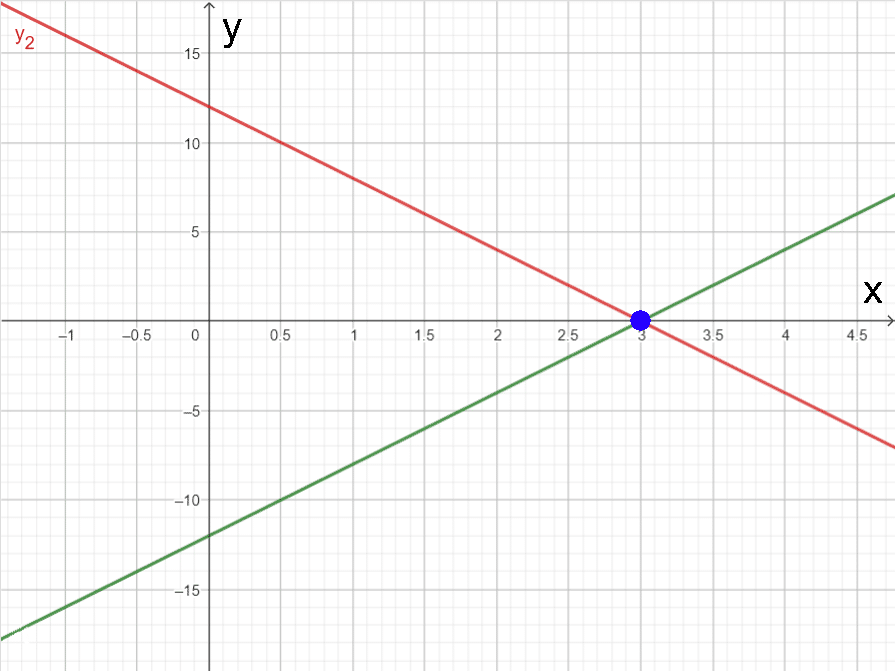
Diese beiden Funktionen kann man nun grafisch darstellen. In beiden Fällen ist die Lösung der gegebenen linearen Gleichung 4·x=12 der Schnittpunkt der Funktionen y1 und y2 mit der x-Achse, also an der Stelle x = 3, weshalb es genügt, nur eine der beiden Funktionen zu zeichnen. Dieser Schnittpunkt ist in der Grafik in blauer Farbe dargestellt:
Beispiel 2: Kompliziertere lineare Gleichung
Berechne x:
$$8+3·x+4·x·(3·x-4)=12·x^2-26·x-18$$
Rechnerische Ermittlung der Lösung
Laut der KLAPUSTRI-Regel sind als Erstes die Klammern aufzulösen. Man erhält:
$$8+3·x+12·x^2-16·x=12·x^2-26·x-18$$
Da auf beiden Seiten der Gleichung der Term 12·x² vorkommt, können wir ihn streichen, indem man ihn auf beiden Seiten abziehen:
$$8+3·x+12·x^2-16·x=12·x^2-26·x-18\qquad / -12·x^2$$
$$8+3·x-16·x=-26·x-18$$
Dadurch kommen in der Gleichung nur noch x vor, es handelt sich also um eine lineare Gleichung. Nun fasst man auf der linken Seite die Terme mit x zusammen und bringt danach alle Terme mit x auf die eine und alle Terme mit reinen Zahlen auf die andere Seite:
$$8-13·x=-26·x-18\qquad / +26·x\quad / -8$$
Man erhält:
$$13·x=-26$$
Nun muss man die Gleichung nur noch durch die Zahl vor dem x dividieren, also durch 13. Somit lautet die Lösung dieser Gleichung:
$$x=-2$$
Probe
Einsetzen der Lösung in die Angabe ergibt:
$$8+3·(-2)+4·(-2)·(3·(-2)-4)=12·(-2)^2-26·(-2)-18$$
Vereinfachen liefert:
$$8-6-8·(-6-4)=12·4+52-18$$
$$2-8·(-10)=48+34\Rightarrow 2+80=82$$
Man erhält eine wahre Aussage und damit ist x=-2 eine Lösung der Gleichung:
$$82=82$$
Seite erstellt am 28.03.2023. Zuletzt geändert am 09.07.2023.