Mit diesem Online-Rechner können Sie exponentielle Prozesse (Wachstum und Abnahme bzw. Zerfall) berechnen und die zugrunde liegende Funktionsgleichung in den beiden üblichen Formen ausgeben lassen. Solche Funktionen heißen Exponentialfunktionen, die von diesem Rechner auch grafisch dargestellt werden. Nach dem Rechner finden Sie Hintergrundinformationen, Formeln und Beispiele zur Anwendung dieses Rechners.
Unter „Auswahl treffen“ können Sie festlegen, welche Größen bekannt sind. Es ist möglich, entweder die Zunahme bzw. Abnahme, den Wachstumsfaktor a oder die Konstante λ einzugeben (im Rechner als „Änderung“ bezeichnet).
Werbung
Rechner für exponentielle Vorgänge
Mit tmin und tmax wird der minimale bzw. der maximale Wert auf der Zeit-Achse festgelegt, also der darzustellende Bereich des Funktionsgraphen. Auch negative Eingaben sind möglich!
* Es kann der Wachstumsfaktor a, die Konstante λ oder die Veränderung in % eingegeben werden. Wählen Sie im Feld darüber eine dieser Möglichkeiten aus, in dem Sie auf den kleinen Pfeil klicken!
** Es kann jede beliebige Einheit für die Zeit verwendet werden: Sekunden, Minuten, Stunden, Tage, Jahre, …
Erklärung der Abkürzungen
| N0 | Startwert/Anfangsmenge |
| N(t) | Wert bzw. Menge zum Zeitpunkt t |
| t | Zeit; es können Minuten, Stunden, Tage, Jahre, … sein |
Mögliche bekannte und gesuchte Größen
- Änderung, Zeit t und Startwert N0 sind bekannt –> N(t) wird berechnet.
- Änderung, Wert zu Beginn N0 und N(t) sind bekannt –> Zeit t wird bestimmt.
- Zeit t und Anfangswert N0 sind bekannt –> Änderung und N(t) werden berechnet.
- Zeit t, Startwert N0 und N(t) sind bekannt –> Änderung wird ermittelt.
Was ist ein exponentielles Wachstum?
Damit man sich die Wirkung eines exponentiellen Wachstums bessser vorstellen kann, nehmen wir an, es liegt eine jährliche Verdopplung vor – also der Wachstumsfaktor a beträgt 2. Am Anfang hat man 1 €. Wieviel Geld hat man nach ein, zwei, drei, vier, … Jahren?
Die Entwicklung des Vermögens zeigen die folgende Wertetabelle und auch die Grafik, die mit dem Rechner erstellt wurde:
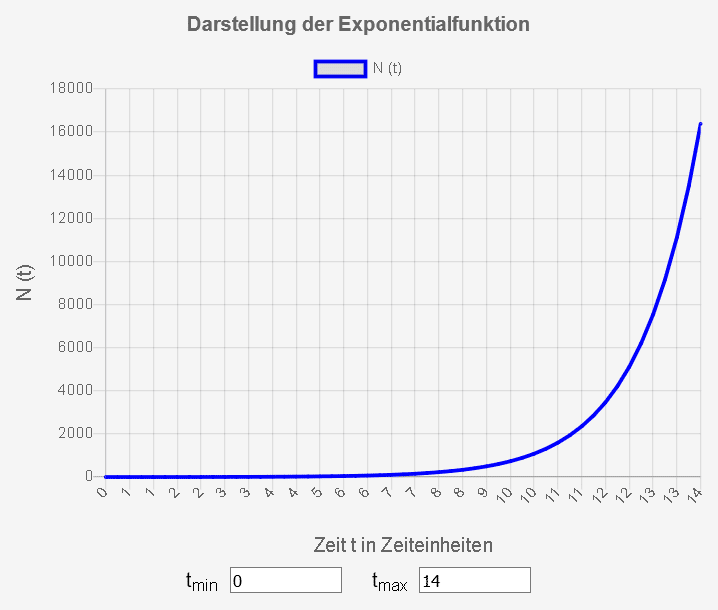
Obwohl sich der Betrag immer jedes Jahr verdoppelt, merkt man am Anfang fast nichts: Ob man nämlich 1 € hat oder 64 €, macht keinen großen Unterschied, denn viel kann man damit ohnehin nicht anfangen. Nach 12 Jahren hätte man jedoch 4096 € und das ist doch eine schöne Menge Geld…
| Jahr | Betrag |
| 0 | 1 |
| 1 | 2 |
| 2 | 4 |
| 3 | 8 |
| 4 | 16 |
| 5 | 32 |
| 6 | 64 |
| 7 | 128 |
| 8 | 256 |
| 9 | 512 |
| 10 | 1024 |
| 11 | 2048 |
| 12 | 4096 |
Kann ein Wachstum immer so weiter gehen?
Nein, das ist natürlich unmöglich, da alles auf der Welt endlich ist. Nur zu Beginn laufen viele Prozesse exponentiell ab. Irgendwann gibt es nämlich einen Wendepunkt und das Wachstum schwächt sich ab, bis ein Höhepunkt erreicht wird. Danach kommt es meist zu einer starken Abnahme.
Beispiel I: Geldanlage
Hätte jemand im Jahr 0 zwei Sesterzen (= Münze im römischen Reich, das entsprach etwa dem täglichen Lohn eines Handwerkers) mit nur 1 % Verzinsung angelegt, dann hätten etwaige Erben heute schon etwas über 1 Milliarde Sesterzen (= 1×109). Wären die zwei Sesterzen hingegen mit 5 % verzinst worden, was durchaus eine realistische Rate bei manchen Anlageformen wie Aktien ist, wäre der Betrag schon auf 1.27×1043 Sesterzen angewachsen. Das ist eine Zahl mit 43 Nullen!
Zum Vergleich: Laut Statista waren im Oktober 2019 insgesamt „nur“ 1.34×1011 Euro-Münzen im Umlauf.
Beispiel II: Besucheranzahl auf meiner Website
Die Besucherzahlen auf meiner Website entwickeln sich seit mittlerweile sechs Jahren exponentiell, sie verdoppeln sich fast jährlich. Ginge das Wachstum noch 10 Jahre so weiter wie bisher, hätte ich im Jahr 2030 Bild.de überholt, was natürlich unmöglich ist.
Formeln für exponentielles Wachstum bzw. Abnahme
Der Funktionswert N(t) zu einem beliebigen Zeitpunkt t kann auf zwei verschiedene Arten berechnet werden:
Formel mit Wachstumsfaktor a
$$N(t)=N_0·a^t$$
Exponentielle Zunahme (Wachstum):
$$a>1$$
Exponentielle Abnahme (Zerfall):
$$a<1$$
Umrechnung zwischen den beiden Formen
Mit den folgenden zwei Formeln ist eine Umrechnung zwischen den beiden Formen möglich. Ist der Faktor a gegeben und die Konstante λ gesucht, verwendet man die linke Formel, im umgekehrten Fall die rechte Formel:
$$\lambda=ln(a) \qquad a=e^\lambda$$
Beispiele für die Anwendung des Rechners
Viele Vorgänge verlaufen in Abschnitten annähernd exponentiell.
Beispiele:
- Einwohnerwachstum einer Stadt bzw. eines Landes
- Verdopplung von Infizierten alle 5 Tage
- Wachstum Anzahl von Bakterien
- Radioaktiver Zerfall: Halbwertszeit bekannt
- Kapitalzuwachs aufgrund einer Verzinsung
- Entwicklung der Besucherzahlen auf meiner Website
Mit exponentiellen Funktionen hat eigentlich jeder Schüler bzw. jede Schülerin zu tun. Fast alle Schulaufgaben können mit diesem Rechner gelöst werden!
Beispiel 1: Einwohner einer Stadt
Im Jahr 2020 wohnen in einer Stadt 25000 Einwohner. Die Einwohnerzahl wächst jährlich um 2 %. Gesucht sind die Einwohner im Jahr 2050 und die Funktionsgleichung.
Lösung:
Bei einer jährlichen prozentuellen Zunahme handelt es sich um ein exponentielles Wachstum.
Man wählt beim Rechner zunächst „Änderung = Zunahme in %“ unter „Änderung, t und N.0 bekannt“ aus. Ins Feld „Zunahme“ trägt man die Zahl 2 ein. Die Zeit t beträgt 30 Jahre (= 2050 – 2020). Zu Beginn lebten 25000 Einwohner in dieser Stadt, also gilt N0 = 25000. Den korrekt ausgefüllten Rechner zeigt der folgende Screenshot:
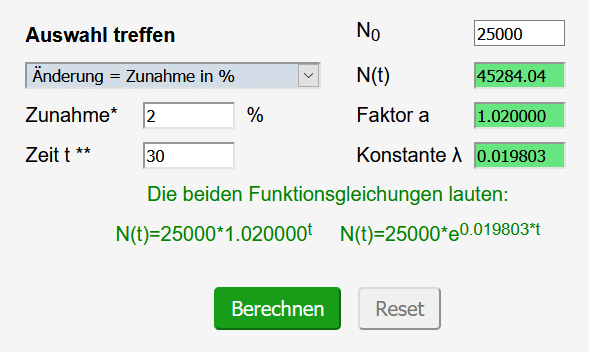
Im Jahr 2050, also zum Zeitpunkt t = 30, wird diese Stadt 45284 Einwohner haben.
Beispiel 2: Coronavirus
Die Zahl der Infizierten verdoppelt sich alle 5 Tage, zu Beginn sind 1 % der Einwohner einer Ortschaft mit 1000 Einwohnern krank. Wie lauten der Wachstumsfaktor und die beiden Funktionsgleichungen? Wie viele Kranke wird es in 30 Tagen geben, wenn keine Maßnahmen ergriffen werden?
Lösung:
1 % von 1000 entspricht 10 Personen. Der Rechner ist also wie folgt auszufüllen:
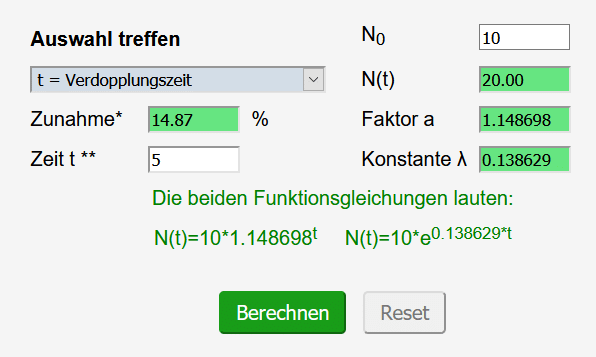
Der Wachstumsfaktor lautet 1.148698.
Zur Berechnung der Infizierten nach 30 Tagen wählt man beim Rechner „Änderung = Zunahme in %“ unter „Änderung, t und N.0 bekannt“ aus. Die Zeit t ist auf 30 zu ändern:
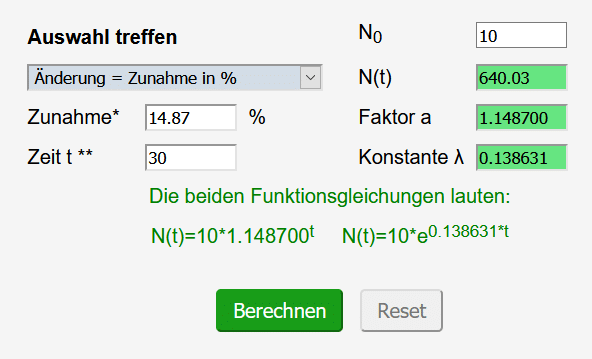
Nach 30 Tagen ohne Maßnahmen wären 640 Personen an Corona erkrankt, also schon fast zwei Drittel der Einwohner!
Beispiel 3: Bakterienwachstum
Zu Beginn existieren 1000 Bakterien. Nach 3 Stunden sind es schon 5000, wobei von einer exponentiellen Zunahme auszugehen ist. Gesucht ist die Funktionsgleichung.
Lösung:
Man wählt beim Rechner zunächst „Eingabe von t, N.0 und N(t)“ unter „t, N.0 und N(t) bekannt“ aus. In die Felder werden die folgenden Zahlen eingetragen:
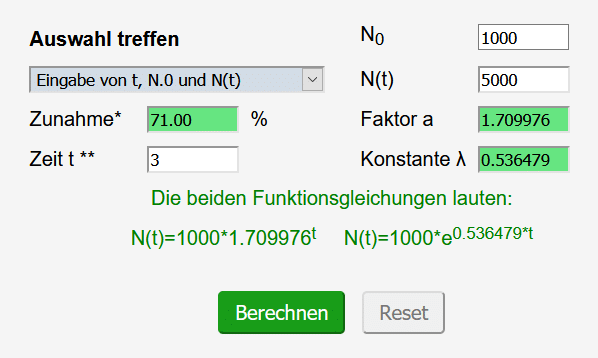
Die Anzahl der Bakterien nimmt also um 71 % pro Stunde zu.
Werbung
Seite erstellt am 24.05.2020. Zuletzt geändert: