Auf dieser Seite findest du die Formeln zur Berechnung der Oberfläche und des Volumens für die wichtigsten Körper wie Quader, Würfel, Drehzylinder, Hohlzylinder, Pyramide, Kegel und Kugel.
Link zu Unterseite:
Inhaltsverzeichnis
Werbung
Prismen & Zylinder
Körper, dessen Grund- und Deckflächen kongruent (das heißt deckungsgleich) und parallel zueinander sind, bezeichnet man als Prisma. Alle Seitenflächen zusammen werden Mantelfläche genannt. Die Grundfläche kann aus beliebigen Vielecken bestehen.
Zylinder besitzen als Grundfläche und Deckfläche einen Kreis. Diese beiden Flächen sind wie beim Prisma deckungsgleich und zueinander parallel.
Allgemeine Formeln für Volumen & Oberfläche
Für Prisma und Zylinder gelten dieselben Formeln.
Für das Volumen V gilt allgemein:
$$V=G \cdot h$$
Volumen = Grundfläche mal Höhe
Für die Oberfläche O gilt allgemein:
$$O=2 \cdot G+M$$
Oberfläche = 2 mal Grundfläche plus Mantelfläche
Tabelle mit Formeln für ausgewählte Prismen und Zylinder
In der folgenden Tabelle sind die Formeln für die wichtigsten Prismen (Quader und Würfel), für den Drehzylinder und den Hohlzylinder zu finden. Die Grundflächen und die Deckflächen sind in den Skizzen grau eingefärbt:
| Körper | Volumen | Oberfläche |
|
|
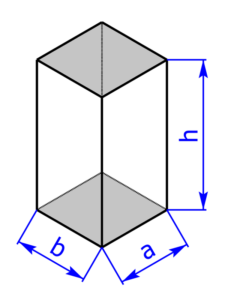
Ein Quader ist ein spezielles Prisma mit einem Rechteck als Grundfläche, dessen Seiten üblicherweise mit a und b bezeichnet werden. Auch bei den vier Seitenflächen, die zusammen die Mantelfläche bilden, handelt es sich um Rechtecke. Alle Flächen stehen aufeinander normal. Zwei gegenüberliegende Flächen sind immer kongruent, also deckungsgleich. Das heißt, es gibt maximal drei verschiedene Flächen. Die Höhe wird mit h bezeichnet. |
|
|
$$V=a⋅b⋅h$$ |
$$O=2⋅(a⋅b+a⋅h+b⋅h)$$ |
|
|
|
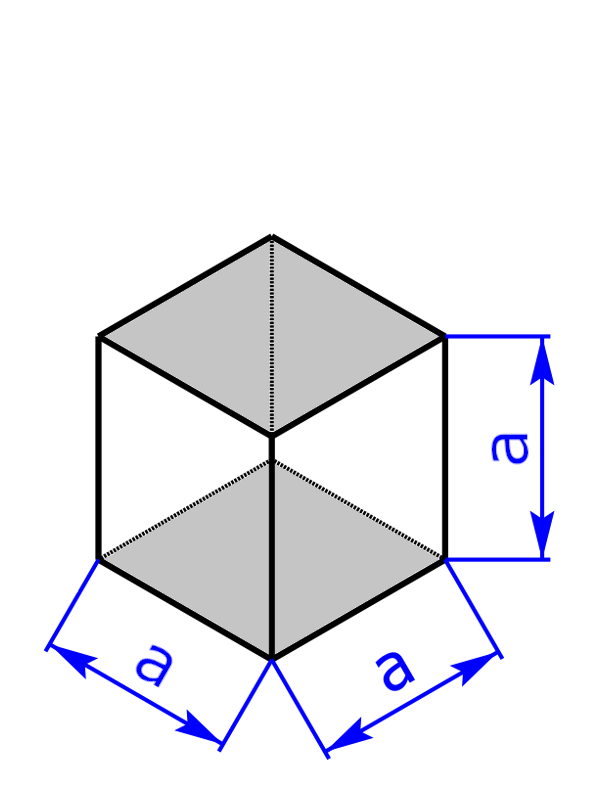
Bei einem Würfel handelt es sich um einen besonderen Quader, bei dem alle Seiten und auch die Höhe gleich lang sind. Es gilt somit: a = b = h. Daher sind auch die sechs Seitenflächen alle gleich groß. Bei diesen Seitenflächen handelt es sich um Quadrate. |
|
|
$$V=a⋅a⋅a=a^3$$ |
$$O=6⋅a⋅a=6⋅a^2$$ |
|
|
|
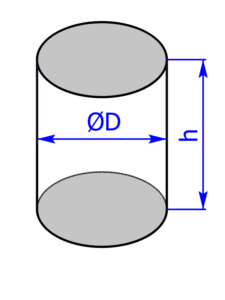
Bei einem Drehzylinder sind sowohl die Grundfläche als auch die Deckfläche ein Kreis. Bei der Mantelfläche handelt es sich um ein Rechteck: Eine Seite dieses Rechtecks ist die Höhe, die andere Seite entspricht dem Umfang des Kreises. Den Radius R in den unten angeführten Formeln bekommt man wie folgt: $$R=\frac{D}{2}$$ |
|
|
$$V=R^2⋅π⋅h$$ |
$$O=2⋅R^2⋅π+2⋅R⋅π⋅h$$ |
|
|
|
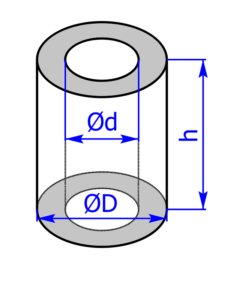
Die Grundfläche und die Deckfläche bestehen bei einem Hohlzylinder aus einem Kreisring. Es handelt sich also um einen Vollzylinder, der in der Mitte ein Loch besitzt. Bei der Berechnung der Oberfläche muss auch die innere Wand berücksichtigt werden. Die Radien R und r bekommt man ähnlich wie beim Drehzylinder. |
|
|
$$V=(R^2−r^2)⋅π⋅h$$ |
$$O=2⋅(R^2−r^2)⋅π+2⋅(R+r)⋅π⋅h$$ |
|
Pyramide & Kegel
Die Pyramide ist ein Körper, dessen Grundfläche ein Polygon ist und dessen Seitenflächen Dreiecke sind. Alle Dreiecke zusammen heißen Mantelfläche. Über dem Mittelpunkt der Grundfläche befindet sich bei einer geraden Pyramide die sogenannte Spitze der Pyramide. Kegel haben als Grundfläche einen Kreis.
Allgemeine Formeln für Volumen & Oberfläche
Für Pyramide und Kegel kommen prinzipiell dieselben Formeln zur Anwendung.
Für das Volumen V gilt allgemein:
$$V=\frac{G \cdot h}{3}$$
Volumen = Grundfläche mal Höhe geteilt durch 3
Für die Oberfläche O gilt allgemein:
$$O=G + M$$
Oberfläche = Grundfläche plus Mantelfläche
Tabelle mit Formeln für ausgewählte Pyramiden und Kegel
In der folgenden Tabelle findest du die Formeln für die wichtigsten Pyramiden (quadratische und rechteckige Pyramide) und für den Drehkegel. Die Grundflächen sind in den Skizzen stets grau eingefärbt:
| Körper | Volumen | Oberfläche |
|
|
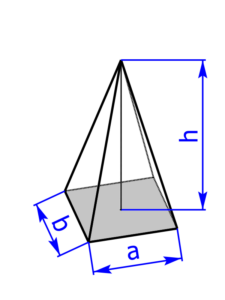
Eine rechteckige (vierseitige) Pyramide hat ein Rechteck als Grundfläche. Bei den vier Seitenflächen, die zusammen die Mantelfläche bilden, handelt es sich um gleichschenkelige Dreiecke. Deren Höhen berechnet man mit dem Satz des Pythagoras. Zwei gegenüberliegende Seitenflächen sind immer kongruent, also deckungsgleich. |
|
|
$$V=\frac{a \cdot b \cdot h}{3}$$ |
$$O=a^2 + a \cdot \sqrt{h^2+ \frac {b^2}{4}}+ b \cdot \sqrt{h^2+ \frac {a^2}{4}}$$ |
|
|
|
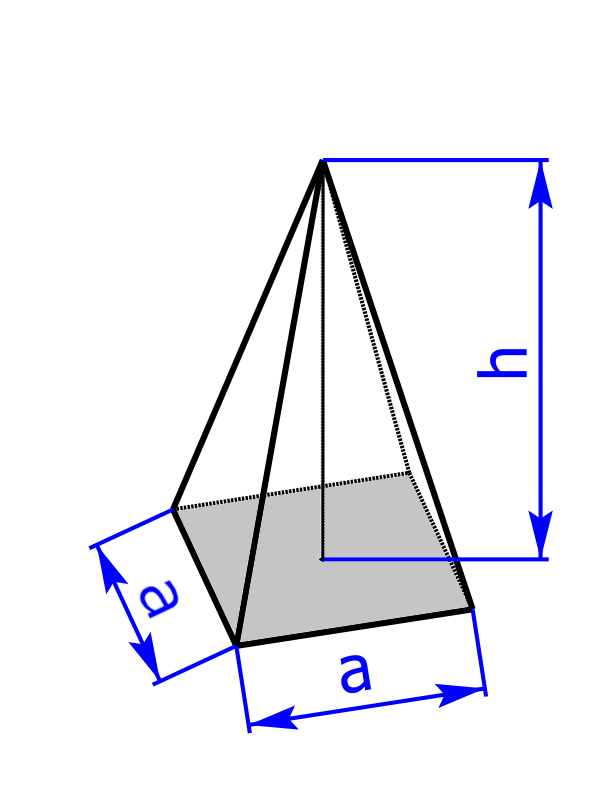
Bei einer quadratischen Pyramide handelt es sich um eine besondere Pyramide, bei der alle vier Seiten gleich lang sind. Es gilt: a = b. Daher sind auch die vier Seitenflächen alle gleich groß. |
|
|
$$V=\frac{a^2 \cdot h}{3}$$ |
$$O=a^2 + a \cdot \sqrt{4 \cdot h^2+a^2}$$ |
|
|
|
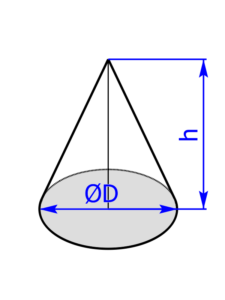
Bei einem Drehkegel ist die Grundfläche ein Kreis und der Mantel ein Kreissektor. Den Radius R in den unten angeführten Formeln bekommt man auf folgende Weise: $$R=\frac{D}{2}$$ |
|
|
$$V=\frac{R^2 \cdot \pi \cdot h}{3}$$ |
$$O=R^2 \cdot \pi + R \cdot \pi \cdot \sqrt{R^2 + h^2}$$ |
|
Kugel
Die Formeln zur Berechnung des Volumens und der Oberfläche einer Kugel lauten:
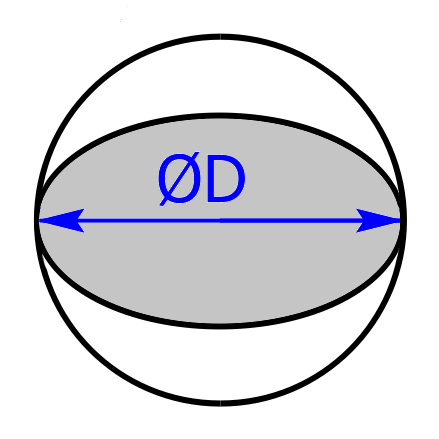
$$V=\frac{4 \cdot R^3 \cdot \pi}{3}$$
$$O=4 \cdot R^2 \cdot \pi$$
$$R=\frac{D}{2}$$
Werbung
Seite erstellt am 13.11.2020. Zuletzt geändert am 18.11.2021.