Auf dieser Seite werden die notwendigen Schritte zur Ermittlung der Auflagerreaktionen eines statisch bestimmten Systems erklärt. Natürlich findet man auch die zur Berechnung benötigten Formeln, also die zwei Kräftegleichgewichtsbedingungen in x- bzw. in y-Richtung und das Momentengleichgewicht.
Zuletzt werden die Auflagerkräfte eines Balkens auf zwei Stützen bestimmt. Auf diesen Balken wirken eine Gleichlast und eine schräge Einzellast. Dieses Beispiel wird komplett durchgerechnet.
Links zu weiteren Unterseiten:
- Balken-Rechner: Mit diesem Rechner können die Auflagerkräfte von einfachen, statisch bestimmt und statisch unbestimmt gelagerten Trägern ermittelt werden.
- Formeln, die der Balkenrechner verwendet (Berechnung von Auflagerreaktionen, Winkel & Durchbiegung)
- Superpositionsprinzip: Berechnung der Auflagerreaktionen mittels Formelsammlung
Inhaltsverzeichnis
- Auflagerreaktionen ermitteln – notwendige Schritte
- Beispiel: Auflagerreaktionen eines Balkens mit Gleichlast und schräger Einzelkraft
Werbung
Auflagerreaktionen ermitteln – notwendige Schritte
Um die Auflagerkräfte bzw. Auflagermomente eines Systems bestimmen zu können, müssen im Allgemeinen folgende Schritte durchgeführt werden:
- Modellbildung und Festlegung eines Koordinatensystems
- System auftrennen / Körper freimachen
- Bei Bedarf Kräfte in ihre Komponenten zerlegen und Resultierende R bilden
- Gleichgewichtsbedingungen aufstellen
- Gleichungssystem lösen
Ein paar der obigen Punkte werden im Folgenden näher erklärt.
System auftrennen / Körper freimachen
Um gesuchte Kräfte bzw. Momente – zum Beispiel Auflagerkräfte – berechnen zu können, ist es erforderlich, ein Gesamtsystem in Teilsysteme aufzutrennen. Diesen Vorgang nennt man auch „Körper freimachen“ oder „Körper freischneiden„. Dabei muss man jedes Bauteil eines Gesamtsystems völlig getrennt betrachten, alle benachbarten Teile lässt man weg und ersetzt sie durch Kräfte und Momente.
Grundlegendes
- Bei ebenen Systemen entstehen an der Trennstelle im Allgemeinen eine Kraft in x-Richtung, eine Kraft in y-Richtung und ein Moment. Deren Größe und Orientierung (= Richtungssinn) ist vorerst unbekannt, zur Berechnung braucht man die sogenannten Gleichgewichtsbedingungen.
- Die sich durch den Schnitt ergebenden Kräfte bzw. Momente sind an beiden Seiten der durchtrennten Körper genau gleich groß, aber entgegengesetzt gerichtet (lateinisch „Actio = Reactio“, drittes newtonsches Axiom), da sie beim Zusammenfügen wieder verschwinden müssen.
Formeln: Gleichgewichtsbedingungen für ebene Probleme
Um die unbekannten Auflagerreaktionen berechnen zu können, braucht man die beiden Kräftegleichgewichtsbedingungen in x- bzw. y-Richtung und das Momentengleichgewicht. Die Formeln für ebene Systeme lauten:
Die Summe aller Kräfte in x-Richtung muss gleich 0 sein (Formel 2.1):
$$\sum F_{i.x}=0$$
Die Summe aller Kräfte in y-Richtung muss gleich 0 sein (Formel 2.2):
$$\sum F_{i.y}=0$$
Die Summe aller Momente um jeden beliebigen Punkt A bezüglich der z-Achse muss gleich 0 sein (Formel 2.3):
$$\sum M_{A.i.z}=0$$
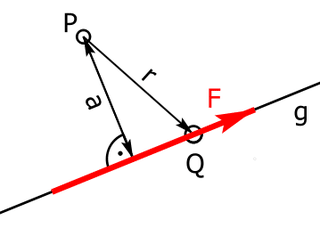
Das Moment Mp einer Einzelkraft F um einen Punkt P berechnet man mit Formel 2.4:
$$M_P = a·F$$
| a | Normalabstand (= kürzeste Entfernung) des Punktes P von der Wirkungslinie g der Einzelkraft F in m. |
| F | Betrag der Einzelkraft in N. |
Es gibt in der Ebene also für jedes (Teil-)System drei Gleichungen, somit können in jedem (Teil-)System maximal drei Unbekannte berechnet werden.
Die gesuchten Auflagerreaktionen (Kräfte bzw. Momente) bekommt man durch Lösen dieses Gleichungssystems.
Beispiel: Auflagerreaktionen eines Balkens
Angabe
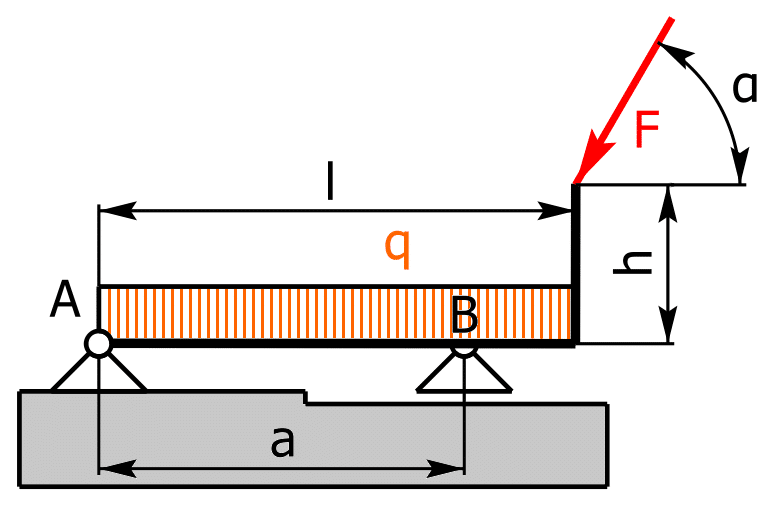
Man betrachte nebenstehende Abbildung eines Balkens, auf den eine Gleichlast q und eine schräge Einzelkraft F unter einem Winkel α wirken. Das linke Lager A ist ein Festlager, Lager B ist als Loslager ausgeführt.
Zahlenwerte:
a = 1.5 m, l = 2 m, h = 0.75 m, α = 60°
Gesucht:
Die Auflagerkräfte in den beiden Lagern A und B
- allgemein
- wenn gilt: q = 2.5 kN/m, F = 8 kN
- wenn gilt: q = 0.5 kN/m, F = 16 kN
Lösung der Aufgabe
Modellbildung und Koordinatensystem
Für diese Aufgabe muss man kein Modell mehr erstellen, da dies schon in der Angabe erledigt wurde. Es gelten unter anderem folgende Idealisierungen:
- Es wurde ein ebenes Modell gewählt.
- Die beiden Lager werden wie üblich als reibungsfrei angenommen.
- Der Körper gilt als starr, das heißt, er verformt sich unter den beiden Krafteinwirkungen nicht.
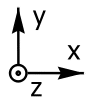
Festlegung des Koordinatensystems:
Die positive x-Achse weist nach rechts, die positive y-Achse zeigt nach oben. Durch die Festlegung der Richtung von x- und y-Achse ist auch die Richtung der z-Achse bekannt: sie muss zum Betrachter hinweisen (Rechtssystem).
Freimachen
Als Erstes macht man den Balken frei. Dazu schneidet man durch die beiden Lager, siehe Skizze.
Festlager A kann Kräfte in x- und in y-Richtung aufnehmen, aber kein Moment, da es reibungsfrei sein soll. Das rechte Loslager B überträgt nur Kräfte in y-Richtung. Die drei blauen Auflagerkräfte A.x, A.y und B.y sind sogenannte Bedingungskräfte, deshalb kennt man ihre Orientierung nicht. Aus diesem Grund können die Pfeilspitzen in beliebiger Richtung eingezeichnet werden.
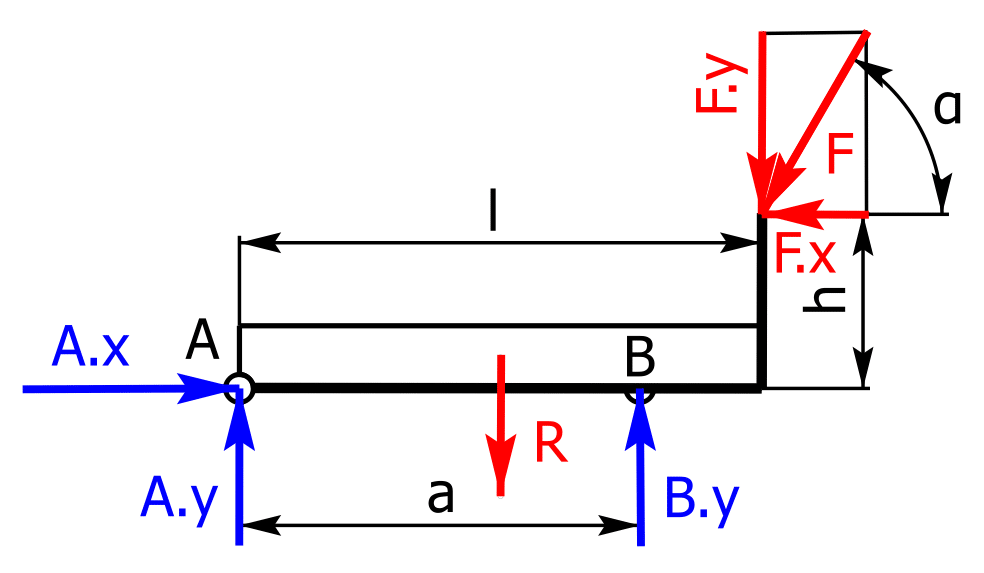
Für die weitere Berechnung gilt: A.x = Ax, A.y = Ay und B.y = By
Resultierende R und Komponenten der Kraft F
Die Gleichlast q muss durch die sogenannte Resultierende R ersetzt werden:
$$R = q·l$$
Die Resultierende R wirkt immer in der Mitte der Gleichlast, hier also im Abstand l/2. Die Einzelkraft F greift schräg an, weshalb sie mithilfe der umgeformten Winkelfunktionen in ihre x- und y-Komponente zerlegt wird:
$$F_x= F·cos(α)\qquad F_y = F·sin(α)$$
Kontrolle:
Nimmt man an, dass gilt α = 90°, bekommt man für die beiden Komponenten:
$$F_x = F·cos(90°) = F·0 \Rightarrow F_x = 0$$
$$F_y = F·sin(90°) = F·1 \Rightarrow F_y = F$$
⇒ Wenn F genau senkrecht zum Balken steht, gibt es keine Komponente in x-Richtung, in y-Richtung wirkt dann die gesamte Kraft F.
Gleichgewichtsbedingungen aufstellen & Gleichungssystem lösen
Nun können die drei Gleichgewichtsbedingungen aufgestellt werden. Jene Kräfte, die in Richtung der positiven Koordinatenachse zeigen, bekommen ein positives Vorzeichen, alle anderen Kräfte sind negativ ins jeweilige Kräftegleichgewicht einzusetzen.
Für die x-Richtung bekommt man mit Formel 2.1:
$$\sum F_{i.x}=0=A_x-F_x$$
Durch Umformen obiger Gleichung erhält man sofort die Auflagerkraft Ax:
$$A_x=F_x \Rightarrow A_x =F·cos(\alpha)$$
Für die y-Richtung erhält man mit Hilfe von Formel 2.2 und einsetzen für R bzw. Fy:
$$\sum F_{i.y} = 0 = A_y + B_y – F_y – R \Rightarrow A_y + B_y – F·sin(α) – q·l = 0$$
Diese Gleichung formt man nach Ay um, da By am einfachsten mit dem Momentengleichgewicht berechnet werden kann:
$$A_y = F·sin(α) + q·l – B_y$$
Zuletzt benötigt man noch die Summe der Momente. Es ist im Prinzip egal, um welchen Punkt man das Momentengleichgewicht bildet. Bei ungünstiger Wahl des Bezugspunktes kann jedoch die Berechnung etwas komplizierter werden.
Mit Formel 2.4 werden die einzelnen Momente berechnet. Das korrekte Vorzeichen ergibt sich mit der sogenannten Rechte-Hand-Regel: Jene Momente, die den Balken um den Punkt A gegen den Uhrzeigersinn verdrehen, bekommen ein positives Vorzeichen, alle anderen Momente sind negativ.
Die Wirkungslinien der beiden Auflagerkräfte Ax und Ay gehen durch den Punkt A, deshalb sind die Normalabstände dieser Kräfte und folglich auch die Momente bezüglich des Punktes A null. Die Summe der Momente um den Punkt A lautet daher:
$$\sum M_{A.i.z} = 0 = – \frac{R·l}{2} + B_y·a – F_y·l + F_x·h$$
Einsetzen für R, Fx und Fy, umformen nach By und herausheben ergibt:
$$B_y=\frac{F·\left[sin(\alpha)·l-cos(\alpha)·h\right]+\frac{q·l^2}{2}}{a}$$
Einsetzen der Zahlenwerte für 2)
Durch Einsetzen der Zahlenwerte in die obigen Gleichungen erhält man die gesuchten Auflagerkräfte:
$$A_x=F_x=F·cos(\alpha) \Rightarrow A_x=8\nobreakspace kN·cos(60°)$$
$$\Rightarrow A_x=4\nobreakspace kN$$
$$B_y=\frac{F·[sin(\alpha)·l-cos(\alpha)·h]+\frac{q·l^2}{2}}{a}$$
$$B_y=\frac{8\nobreakspace kN·[sin(60°)·2\nobreakspace m-cos(60°)·0.75\nobreakspace m]+\frac{2.5\nobreakspace \frac{kN}{m}·(2\nobreakspace m)^2}{2}}{1.5 \nobreakspace m}$$
$$\Rightarrow B_y=10.571\nobreakspace kN$$
$$A_y=F·sin(\alpha)+q·l-B_y \Rightarrow A_y=8\nobreakspace kN·sin(60°)+2.5\nobreakspace\frac{kN}{m}·2\nobreakspace m-10.571kN$$
$$\Rightarrow A_y=1.357\nobreakspace kN$$
Einsetzen der Zahlenwerte für 3)
$$A_x=16\nobreakspace kN·cos(60°)\Rightarrow A_x=8\nobreakspace kN$$
$$B_y=\frac{16\nobreakspace kN·[sin(60°)·2\nobreakspace m-cos(60°)·0.75\nobreakspace m]+\frac{0.5\nobreakspace \frac{kN}{m}·(2\nobreakspace m)^2}{2}}{1.5\nobreakspace m}\Rightarrow B_y=15.142\nobreakspace kN$$
$$A_y=16\nobreakspace kN·sin(60°)+0.5\nobreakspace\frac{kN}{m}·2\nobreakspace m-15.142\nobreakspace kN\Rightarrow A_y=-0.286\nobreakspace kN$$
Diesmal ist die Auflagerkraft Ay negativ, daher wirkt sie tatsächlich in die entgegengesetzte Richtung als angenommen.
Werbung
Seite erstellt am 14.05.2019. Zuletzt geändert am 11.11.2021.