Dieser Online-Rechner berechnet die Massenträgheitsmomente (kurz als Trägheitsmoment oder auch als Inertialmoment bezeichnet, früher Drehmasse), die Masse und das Volumen von 14 verschiedenen Körpern. Als Werkstoff stehen Stahl, Aluminium und unterschiedliche Holzarten zur Auswahl. Folgende Körper sind verfügbar:
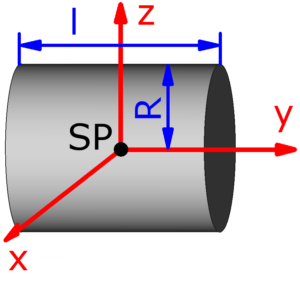
- Vollzylinder
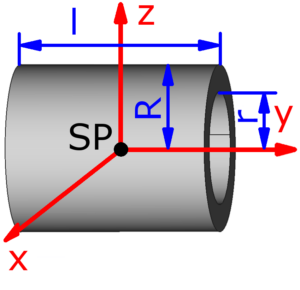
- Hohlzylinder
- Zylindermantel
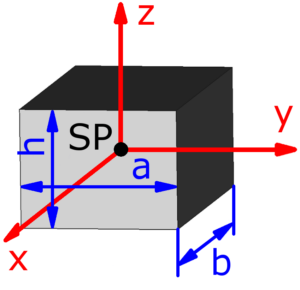
- Quader
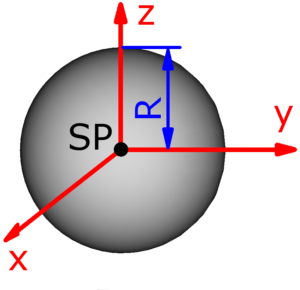
- Kugel
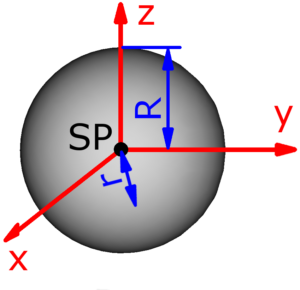
- Hohlkugel
- Kugelschale
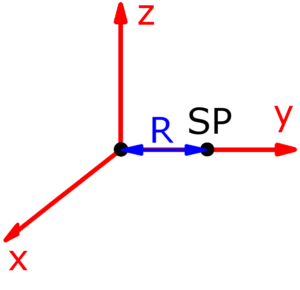
- Punktmasse
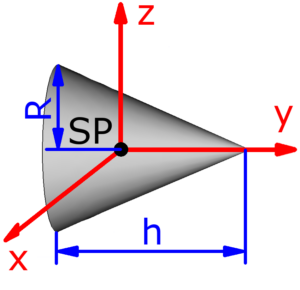
- Vollkegel
- Kegelmantel
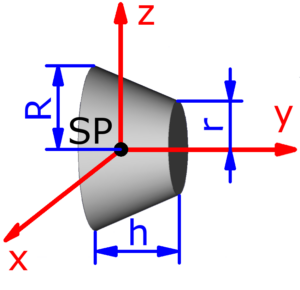
- Kegelstumpf
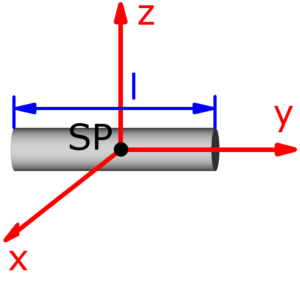
- schlanker Stab (R = 0)
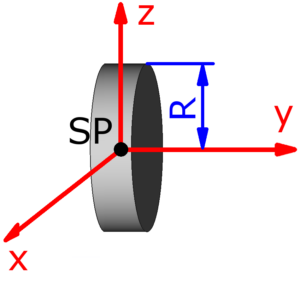
- dünne Scheibe (l = 0)
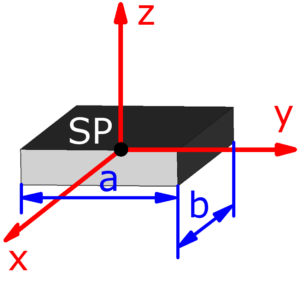
- dünne Platte (h = 0)
Links zu Unterseiten:
- Formeln zur Berechnung der Massenträgheitsmomente
- Beispiel: Berechnung des Massenträgheitsmoments einer Riemenscheibe
Werbung
Massenträgheitsmoment-Rechner
Mit der Voreinstellung werden die Massenträgheitsmomente, die Masse und das Volumen für einen Vollzylinder aus Stahl berechnet.
* Eine homogene Dichte wird bei allen Körpern vorausgesetzt. Die Dichte wird automatisch durch die Auswahl eines Werkstoffs berechnet. Es ist jedoch auch die Eingabe individueller Werte möglich!
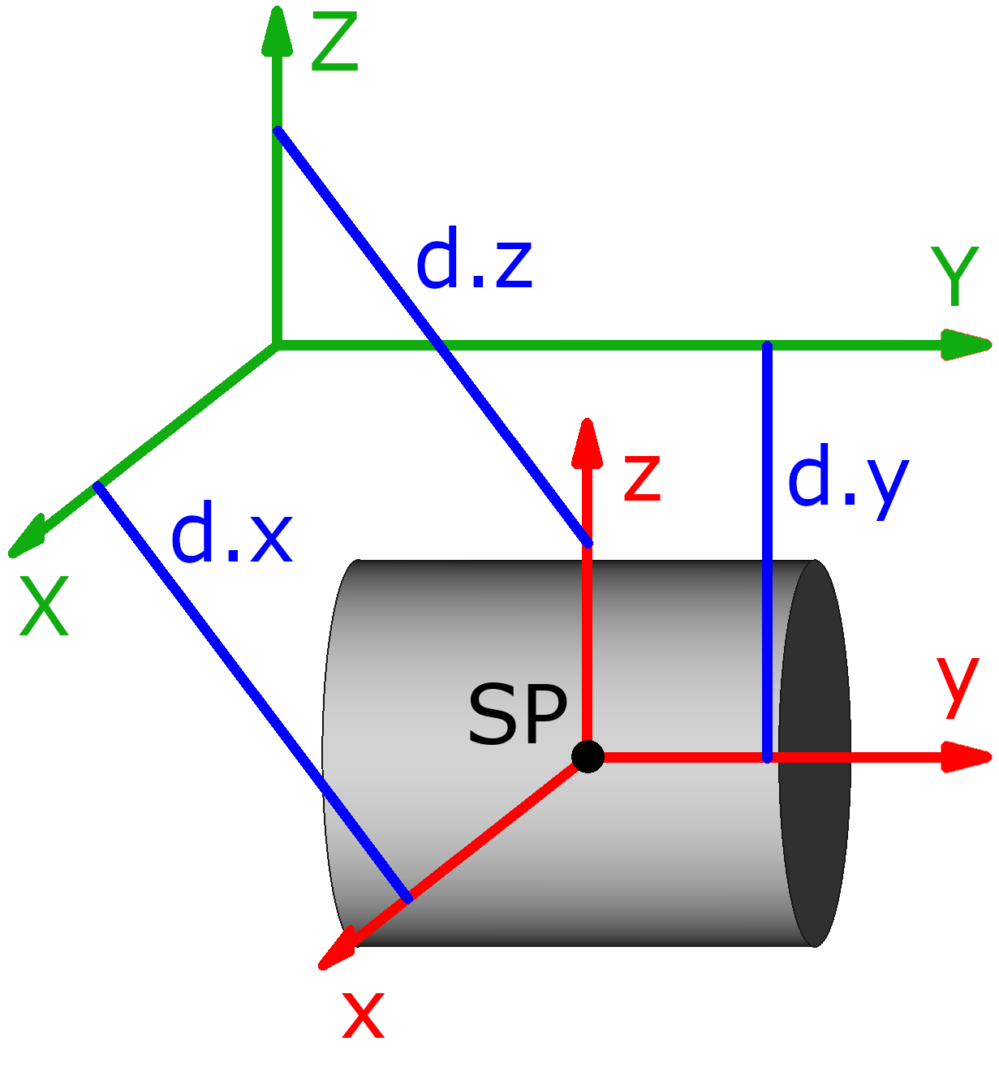
** Die Längen dx, dy und dz sind die Abstände zwischen den jeweiligen Drehachsen, siehe „Zusammengesetzte Massenträgheitsmomente“ weiter unten auf dieser Seite.
Hinweise für die Verwendung des Rechners
- Die roten Pfeile sind die Koordinatenachsen und stellen zugleich auch die Drehachsen dar. Jx ist zum Beispiel das Trägheitsmoment, wenn sich der Körper um die x-Achse dreht. Die Drehachsen verlaufen – außer bei der Punktmasse – stets durch den mit SP bezeichneten Schwerpunkt des jeweiligen Körpers, der zugleich der Koordinatenursprung ist.
- Die Querschnitte müssen immer symmetrisch zu der durch jeweils zwei Koordinatenachsen aufgespannten Ebene sein – das sind die xy-, die yz- und die xz-Ebene. Davon ausgenommen sind die Punktmasse und kegelförmige Körper, die nur bezüglich der xy- und der yz-Ebene symmetrisch sind.
- Die Trägheitsmomente Jx und Jz können für Kegelmantel und Kegelstumpf nicht berechnet werden!
- Auch die Massenträgheitsmomente von dünnen Scheiben, schlanken Stäben oder dünnen Platten können mit diesem Rechner bestimmt werden. In diesem Fall wird die Länge l, die Höhe h oder der Radius R gleich 0 gesetzt und kann nicht mehr geändert werden. Zudem muss eine korrekte Masse eingegeben werden.
- Für die richtige Funktion kann keine Gewähr übernommen werden – für Berichtigungen und Verbesserungsvorschläge bitte um Nachricht mittels Kontaktformular!
Zusammengesetzte Massenträgheitsmomente
Oft ist es günstig, einen komplexen Körper aus mehreren Teilkörpern zusammenzusetzen. Die Massenträgheitsmomente dieser Teilkörper können beliebig addiert bzw. auch subtrahiert werden, sofern alle Schwerpunkte auf derselben Drehachse liegen. Das Trägheitsmoment eines Hohlzylinders kann man zum Beispiel durch das Bilden der Differenz der Trägheitsmomente von zwei Vollzylindern mit unterschiedlichen Radien berechnen.
Möchte man hingegen das Massenträgheitsmoment eines Körpers bezüglich einer beliebigen, parallel verschobenen Drehachse bestimmen, wird der sogenannte Satz von Steiner benötigt. Zur Berechnung dieser Trägheitsmomente braucht man die Abstände dx, dy oder dz, siehe Abbildung.
Rechenbeispiel (auch Anwendung des Satz von Steiner):
Skizzen der verfügbaren Körper
Die folgenden 14 Körper können beim Massenträgheitsmoment-Rechner ausgewählt werden. Die Formeln zur Berechnung findet man auf einer eigenen Seite:



Werbung
Seite erstellt im Februar 2019. Zuletzt geändert am: