Auf dieser Seite findest du die Energie- bzw. Bernoulligleichung zur Berechnung von der Geschwindigkeit, dem Höhenunterschied oder dem Druck in Rohren. Auch die Reibung in den Rohren und die Reibung von Rohrleitungseinbauten (Krümmer, Ventile, Querschnittsveränderungen, Einläufe) kann in der Formel berücksichtigt werden.
Zudem werden hier die Formeln zur Berechnung des Ausflusses von Gefäßen, die Formeln zur Berechnung des Massenstromes und des Volumenstromes (=Durchfluss) – die sogenannte Kontinuitätsgleichung – und die Formel für die Strahl-Stoßkraft angegeben. Die Formel für den Ausfluss aus einem oben offenen Gefäß (Torricelli-Gleichung) wird in einem kurzen Beispiel hergeleitet.
Link zu Unterseite:
- Rechner (in Arbeit!)
Inhaltsverzeichnis
- Übersichtstabelle
- Energiegleichung & Bernoulligleichung
- Formel der Energiegleichung
- Notwendige Voraussetzungen
- Reibungsfreie Bernoulligleichung
- Erweiterte Bernoulligleichung für reibungsbehaftete Strömungen
- Atmosphärischer Druck, Absolutdruck & Überdruck
- Formeln für den Ausfluss aus Gefäßen
- Massenstrom, Kontinuitätsgleichung & Volumenstrom
- Strahl-Stoßkraft
Werbung
Übersichtstabelle (in ARBEIT!!)
In dieser Tabelle sind die wichtigsten Formeln zu finden. Für genauere Informationen sei auf die folgenden Abschnitte verwiesen.
| Bernoulligleichung | Formel | |
| spezifische Energiegleichung | $$\frac{v_1^2}{2}+\frac{p_1}{\rho}+g·h_1=\frac{v_2^2}{2}+\frac{p_2}{\rho}+g·h_2$$ | |
| Druckgleichung | $$\frac{v_1^2·\rho}{2}+p_1+\rho·g·h_1 = \frac{v_2^2·\rho}{2}+p_2+\rho·g·h_2$$ | |
| Höhengleichung | $$\frac{v_1^2}{2·g}+\frac{p_1}{\rho·g}+h_1= \frac{v_2^2}{2·g}+\frac{p_2}{\rho·g}+h_2$$ | |
| mit Verlusten | $$\frac{v_1^2}{2}+\frac{p_1}{\rho}+g·h_1=\frac{v_2^2}{2}+\frac{p_2}{\rho}+g·h_2+\sum\zeta·\frac{v^2}{2}+\sum\lambda·\frac{l}{d}·\frac{v^2}{2}$$ | |
| Ausfluss aus Gefäßen | oben offen | oben geschlossen |
| $$v_a=\sqrt{2·g·h}$$ | $$v_a=\sqrt{2·\left(\frac{p_e}{\rho}+g·h\right)}$$ | |
| Kontinuitätsgleichung | Volumenstrom | |
|
$$A_1·v_1=A_2·v_2$$ |
$$\dot{V}=A·v$$ | |
Energiegleichung & Bernoulligleichung
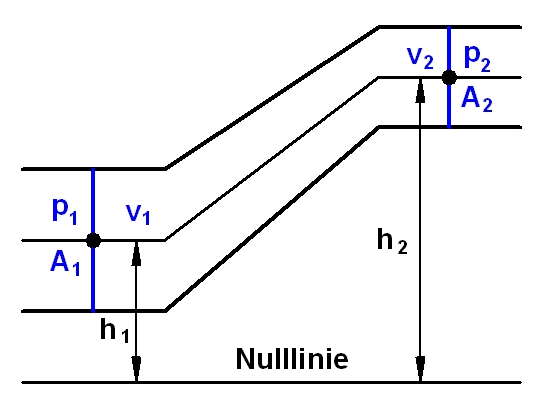
Die Energie- bzw. Bernoulligleichung vergleicht die Zustände von zwei verschiedenen Punkten einer Stromlinie, siehe Abbildung. Die Gesamtenergie bleibt über die gesamte betrachtete Länge konstant und setzt sich aus den folgenden drei Teilenergien zusammen:
- kinetische Energie
- Druckenergie
- potentielle Energie
Formel der Energiegleichung
Die Energiegleichung lautet daher bei reibungsfreier Strömung:
$$\frac{m·v_1^2}{2}+p_1·V+m·g·h_1=\frac{m·v_2^2}{2}+p_2·V+m·g·h_2$$
| m | Masse in kg |
| v1, v2 | Mittlere Geschwindigkeit im Querschnitt 1 bzw. 2 in m/s |
| p1, p2 | Druck an der Stelle 1 bzw. 2 in Pascal: 1 Pa = 1 N/m², 105 Pa = 1 bar |
| V | Volumen in m³ |
| g | Erdbeschleunigung, g = 9.81 m/s² |
| h1, h2 | Abstände vom Nullniveau zum Mittelpunkt des Rohres in m |
| A1, A2 | Querschnittsflächen in m² (für Kontinuitätsgleichung) |
Das Nullniveau (in der Skizze mit Nulllinie bezeichnet) kann beliebig gewählt werden. Je nach Lage der Nulllinie können die Abstände auch negativ werden. Meist ist es günstig, die Nulllinie in den tiefsten der beiden Punkte zu legen, da so in der Gleichung eine Höhe verschwindet und nur positive Abstände vorkommen. Die Geschwindigkeit v wird oft auch mit c bezeichnet.
Notwendige Voraussetzungen
Notwendige Voraussetzung für die Verwendung der Bernoulli- bzw. Energiegleichung ist sowohl eine stationäre Strömung als auch eine inkompressible und viskositätsfreie Flüssigkeit, wobei jedoch die Reibung berücksichtigt werden kann.
Das heißt also, dass
- die Geschwindigkeit der Strömung an jedem Ort zeitlich gleich groß bleibt (es darf aber Orte mit unterschiedlichen Geschwindigkeiten geben!),
- sich die Dichte nicht ändern darf – also konstant zu bleiben hat,
- und dass es sich um ein dünnflüssiges Medium wie etwa Wasser handeln muss.
Reibungsfreie Bernoulligleichung
Die oben angeführte Energiegleichung ist in der Praxis meist nicht relevant. Stattdessen verwendet man drei spezielle Formen der Energiegleichung, die man auch Bernoulligleichung nennt: Spezifische Energiegleichung, Druckgleichung und Höhengleichung.
Spezifische Energiegleichung
Verwendet man die Formel V=m/ρ und dividiert anschließend die Energiegleichung durch die Masse, erhält man die spezifische Energiegleichung. Bei einer reibungsfreien Strömung lautet die Formel:
$$\frac{v_1^2}{2}+\frac{p_1}{\rho}+g·h_1=\frac{v_2^2}{2}+\frac{p_2}{\rho}+g·h_2$$
| v1, v2 | Mittlere Geschwindigkeit im Querschnitt 1 bzw. 2 in m/s |
| p1, p2 | Druck an der Stelle 1 bzw. 2 in Pascal: 1 Pa = 1 N/m², 105 Pa = 1 bar |
| ρ | Dichte des Fluids in kg/m³ |
| g | Erdbeschleunigung, g = 9.81 m/s² |
| h1, h2 | Abstände vom Nullniveau zum Mittelpunkt des Rohres in m |
Druckgleichung
Multipliziert man die spezifische Energiegleichung mit der Dichte ρ, erhält man die sogenannte Druckgleichung:
$$\frac{v_1^2·\rho}{2}+p_1+\rho·g·h_1 = \frac{v_2^2·\rho}{2}+p_2+\rho·g·h_2$$
Höhengleichung
Dividiert man die spezifische Energiegleichung durch g, erhält man die Formel für die Höhengleichung:
$$\frac{v_1^2}{2·g}+\frac{p_1}{\rho·g}+h_1= \frac{v_2^2}{2·g}+\frac{p_2}{\rho·g}+h_2$$
Erweiterte Bernoulligleichung für reibungsbehaftete Strömungen
Die sogenannte erweiterte Bernoulligleichung auf Basis der spezifischen Energiegleichung berücksichtigt auch die Reibung in den Rohren sowie die Druckverluste von Rohrleitungseinbauten wie Schieber oder Ventilen und von Rohrkomponenten wie Krümmer/Bögen, Knien, Einläufe, Ausläufe, Abzweigungen, Vereinigungen, Verengungen und Erweiterungen:
$$\frac{v_1^2}{2}+\frac{p_1}{\rho}+g·h_1=\frac{v_2^2}{2}+\frac{p_2}{\rho}+g·h_2+\sum\zeta·\frac{v^2}{2}+\sum\lambda·\frac{l}{d}·\frac{v^2}{2}$$
| ζ | Druckverlustbeiwert oder Widerstandsbeiwert (dimensionslos) |
| v | Geschwindigkeit an der Stelle der Einbauten und Komponenten bzw. im Rohr in m/s |
| λ | Rohrreibungszahl (dimensionslos) |
| l | Länge der Rohrleitung in m |
| d | Rohrdurchmesser in m |
Das Zeichen ∑ ist das sogenannte Summenzeichen. Es besagt, dass alle Verluste aufsummiert werden müssen. Bei gleichen Querschnitten bzw. Durchmessern und damit gleichen Geschwindigkeiten können die Widerstandsbeiwerte ζ einfach addiert werden.
Druckverlustbeiwert oder Widerstandsbeiwert ζ
Den dimensionslosen Druckverlustbeiwert oder Widerstandsbeiwert ζ für Rohrleitungseinbauten und Komponenten kommt man aus Tabellen (z. B. hier zu finden) oder durch Googeln.
Dieser Beiwert kann auch durch Versuche ermittelt werden, wenn die Druckdifferenz Δp = pvor – pnach mittels zweier Manometer gemessen wird – wobei pvor der Druck am Manometer vor der Komponente ist und pnach der Druck am Manometer nach der Komponente ist. Die Formel zur Berechnung des Widerstandsbeiwerts lautet:
$$\zeta=\frac{\Delta p}{\frac{\rho·v^2}{2}}=\frac{p_{vor}-p_{nach}}{\frac{\rho·v^2}{2}}$$
Rohrreibungszahl λ
Die Rohrreibungszahl λ hängt bei turbulenten Strömungen von der Rauheit k des Rohrs, vom Rohrdurchmesser d und von der Reynoldszahl Re ab. Sie wird meist aus Diagrammen ermittelt, die man zum Beispiel auf Wikipedia findet. Für laminare Strömungen – also für eine Reynoldszahl Re < 2300 – gilt der folgende Zusammenhang:
$$\lambda=\frac{64}{Re}$$
Reynoldszahl Re
Die Reynoldszahl Re wird mit der folgenden Formel berechnet, wobei ν die kinematische Viskosität ist:
$$Re=\frac{v·d}{\nu}$$
Für Wasser bei einer Temperatur von 20 °C gilt: ν = 10-6 m2/s.
Atmosphärischer Druck, Absolutdruck & Überdruck
Es besteht folgender Zusammenhang zwischen dem atmosphärischen Druck pamb, dem Absolutdruck pabs und dem Überdruck pe:
$$p_{abs}=p_{amb}+p_e$$
Relativdruck bzw. Überdruck pe
Der Überdruck oder Relativdruck wird meist mit pe bezeichnet, wobei das kleine e für excedens = überschreitend steht. Er ist die Differenz zwischen dem absoluten Druck und dem aktuellen atmosphärischen Druck und kann durch Umformen der obigen Formel berechnet werden:
$$p_e=p_{abs}-p_{amb}$$
Ein negativer Überdruck wurde früher als Unterdruck bezeichnet. Das bedeutet, dass der Überdruck kleiner als der atmosphärische Druck ist. Der Überdruck wird durch das Wetter und die Seehöhe – meist geringfügig – beeinflusst, da sich auch der atmosphärische Druck ändert!
Klassische Manometer zeigen in der Regel den Überdruck an. Beispiel: Das Manometer einer Fahrradpumpe gibt im nicht angeschlossenen Zustand 0 bar aus. Oft wird praktischerweise nur mit dem Überdruck gerechnet, indem man einfach den atmosphärischen Druck mit 0 bar annimmt.
Atmosphaerischer Druck pamb
Die Bezeichnung für den atmosphärischen Druck ist pamb, wobei amb für ambiens = umgebend verwendet wird. Er nimmt mit zunehmender Seehöhe ab und wird auch durch die aktuelle Wetterlage verändert. Man kann näherungsweise mit pamb = 1000 hPa = 1 bar rechnen.
Formeln für den Ausfluss aus Gefäßen
Man unterscheidet zwischen oben offenen und oben geschlossenen Gefäßen.
Ausfluss aus einem oben offenen Gefäß (Torricelli-Gleichung)
Mithilfe der Bernoulligleichung kann die Formel für die Ausflussgeschwindigkeit va aus einem oben offenen Behälter – zum Beispiel aus einem Stausee oder Tank – ermittelt werden:
$$v_a=\sqrt{2·g·h}$$
Diese Formel ist auch unter dem Namen Torricelli-Gleichung bekannt.
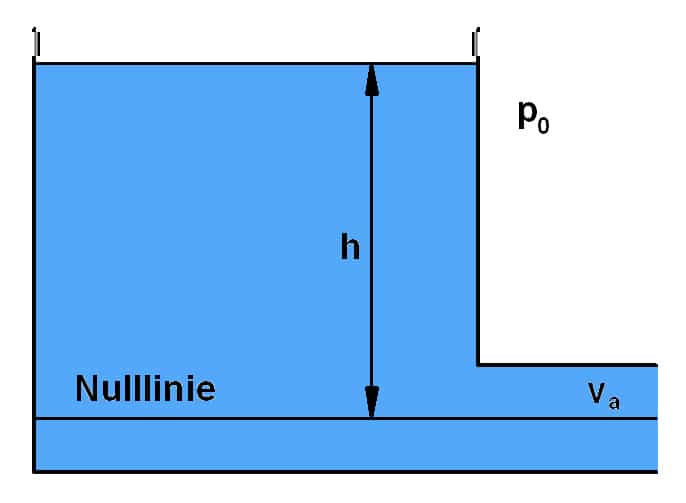
Beispiel: Herleitung dieser Formel
Zur Herleitung geht man von der Bernoulligleichung aus:
$$\frac{v_1^2}{2}+\frac{p_1}{\rho}+g·h_1=\frac{v_2^2}{2}+\frac{p_2}{\rho}+g·h_2$$
Die Größen mit dem Index 1 gelten an der Wasseroberfläche, die Größen mit dem Index 2 am Ausfluss. An der Oberfläche ist die Geschwindigkeit v1 (fast) null. Je größer der obere Querschnitt, desto eher trifft diese Idealisierung zu. Legt man das Nullniveau in den Ausfluss, ist h2 null und h1 entspricht dem Höhenunterschied h. Der Umgebungsdruck p0 ist oben und unten annähernd gleich groß. Somit vereinfacht sich die Bernoulli-Gleichung:
$$\frac{p_0}{\rho}+g·h=\frac{v_2^2}{2}+\frac{p_0}{\rho}$$
Da der Druck p0 gleich groß ist, fällt er aus der Gleichung heraus. Bezeichnet man v2 als va und formt noch nach der Geschwindigkeit um, erhält man:
$$g·h=\frac{v_a^2}{2}\Rightarrow v_a=\sqrt{2·g·h}$$
Ausfluss aus einem oben geschlossenen Gefäß
Mithilfe der Bernoulligleichung kann auch die Formel für die Ausflussgeschwindigkeit va aus einem oben geschlossenen Behälter bestimmt werden:
$$v_a=\sqrt{2·\left(\frac{p_e}{\rho}+g·h\right)}$$
Mit pe wird der Überdruck im Gefäß bezeichnet (Einheit: Pascal).
Massenstrom, Kontinuitätsgleichung & Volumenstrom
In diesem Abschnitt findest du die Formeln zur Berechnung des Massenstromes und des Volumenstromes. Zudem wird auch die Kontinuitätsgleichung angegeben.
Massenstrom
Der Massenstrom wird mit der folgenden Formel berechnet:
$$\dot{m}=\rho·A·v$$
Den Massenstrom bekommt man also durch das Produkt aus Dichte ρ, Querschnittsfläche A und Geschwindigkeit v. Die SI-Einheit des Massenstromes ist kg/s. Dazu ist die Dichte in kg/m³, die Fläche in m² und die Geschwindigkeit in m/s einzusetzen.
Kontinuitätsgleichung
Der Massenstrom muss über den gesamten Abschnitt der Stromlinie konstant bleiben, da keine Massenanteile verloren gehen können. Aus diesem Grund lautet die Kontinuitätsgleichung:
$$\rho_1·A_1·v_1=\rho_2·A_2·v_2$$
Wenn das Fluid zudem inkompressibel ist – also die beiden Dichten ρ1 und ρ2 annähernd gleich groß sind – vereinfacht sich die obige Gleichung noch etwas, da die Dichte in diesem Fall herausgekürzt werden kann. Man erhält die folgende Formel:
$$A_1·v_1=A_2·v_2$$
Volumenstrom (Durchfluss)
Das Produkt aus Querschnitt A und Geschwindigkeit v der Flüssigkeit wird als Volumenstrom oder Durchfluss bezeichnet:
$$\dot{V}=A·v$$
Die SI-Einheit des Volumenstromes ist m³/s, oft wird aber auch l/s oder l/min verwendet. Für „V Punkt“ ist häufig auch die Bezeichnung Q anzutreffen:
$$Q=A·v$$
Strahl-Stoßkraft
Die Kraft, die ein Strahl auf eine senkrechte Wand ausübt, wird mit der folgenden Formel berechnet:
$$F=\dot{m} · v=\rho · A · v^2$$
Als Einheit der Stoßkraft F bekommt man Newton, wenn man für die anderen Größen die SI-Einheiten einsetzt.
Werbung
Seite erstellt am 20.01.2022. Zuletzt geändert am 29.01.2023.