Diese Seite auf Deutsch: Formeln für Geschwindigkeit, Beschleunigung, Weg und Zeit
On this page you will find all formulas for the calculation of speed, acceleration, distance and time with or without initial speed. At the end of the page there is an example for a better understanding of these formulas, in which the acceleration, the final velocity and the average velocity are calculated.
Links to subpages:
- Calculator for distance, velocity, acceleration and time (Stopping Distance Calculator)
- Acceleration Calculator
Formulas for Average Velocity, Distance and Time
The following formulas can be used to calculate the average speed v, the distance s or the time t required, where the average speed is constant.The first formula with the delta sign Δ represents the correct mathematical notation and is also called the difference quotient, because the difference between the distances is divided by the time difference. Often, however, the delta sign is left out – see the simplified formulas in the next section.
$$v=\frac{\Delta s}{\Delta t}=\frac{s(t_1)-s(t_0)}{t_1-t_0}=\frac{s_1-s_0}{t_1-t_0}=\frac{distance}{time\ required}$$
$$\Delta s= v·\Delta t\qquad \Delta t =\frac{\Delta s}{v}$$
Meaning of the Variables
| v | average velocity in m/s in the interval [t0; t1] (‘velocity’, therefore the abbreviation v) |
| s or Δs |
distance or route in m in the interval [t0; t1]; sometimes d is used instead of s |
| t or Δt | time required (= time difference) in s (‘time’, therefore the abbreviation t) |
| s(t0) or s0 | distance at time t0 (starting point); s0 and t0 are often 0) |
| s(t1) or s1 | distance at time t1 (destination) |
Simplified notation of these formulas
The above formulas are known in a simplified notation, too. However, you have to keep in mind that distance and time are differences, see also the following examples on this page:
This fact can be ignored if the starting distance s0 and the starting time t0 are equal to 0.
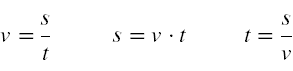
Attention to the units:
The units must always fit together! To convert a speed v given in km/h into m/s, simply divide the speed by 3.6:
$$v = 18\ km/h \Rightarrow \frac{18}{3.6} \Rightarrow v = 5\ \frac{m}{s}$$
The opposite is done in a similar way: If you multiply a speed v given in m/s by 3.6, you get the same speed in km/h:
$$v = 10\ m/s \Rightarrow 10⋅3.6 \Rightarrow v = 36\ km/h$$
Other possibility:
If you take distance in km and time in h, you get speed in km/h.
Formulas for Average Acceleration
The average acceleration a, the change in velocity v or the required time t can be calculated by using the following formulas, whereby the average acceleration is constant:
$$a=\frac{\Delta v}{\Delta t}=\frac{v(t_1)-v(t_0)}{t_1-t_0}=\frac{v_1-v_0}{t_1-t_0}=\frac{change\ of\ velocity}{time\ required}$$
$$\Delta v= a·\Delta t\qquad \Delta t =\frac{\Delta v}{a}$$
Meaning of the Variables
| a | average acceleration in m/s² in the interval [t0; t1] (‘velocity’, therefore the abbreviation v) |
| Δv | change of velocity (= velocity difference) in m/s in the interval [t0; t1] |
| Δt | time required in s |
| v(t0) or v0 | velocity at time t0 (starting or initial velocity); v0 and t0 are often 0 |
| v(t1) or v1 | velocity at time t1 (final velocity) |
Notes on the formulas and especially on differences
- A negative value for the acceleration means that the vehicle is actually braking or decelerating.
- The following formulas are based on the definition above of the average acceleration or its integral. The speed at time t0 is called the initial speed v0 and the speed at time t1 is called the final velocity v.
- The time difference Δt and the distance difference Δs are represented in a simplified manner by t and s. If s(t0) and t0 are equal to 0, one can ignore the fact that distance and time are actually differences. A starting point s0 is therefore not taken into account in the formulas, as it is not relevant for most tasks. However, it is possible to replace the distance s by the term s – s0, as the following example shows.
- Below you find another example of calculating a time difference.
Formulas for Uniform Acceleration – Starting Velocity = 0
These formulas apply to constant acceleration or deceleration, whereby both the initial velocity and the initial distance must be zero.
In principle, these are the same formulas as in the following section, but the initial speed v0 is set to zero. The 5th line is completely omitted due to the missing initial speed v0.
Please note the hint on differences in the previous chapter!
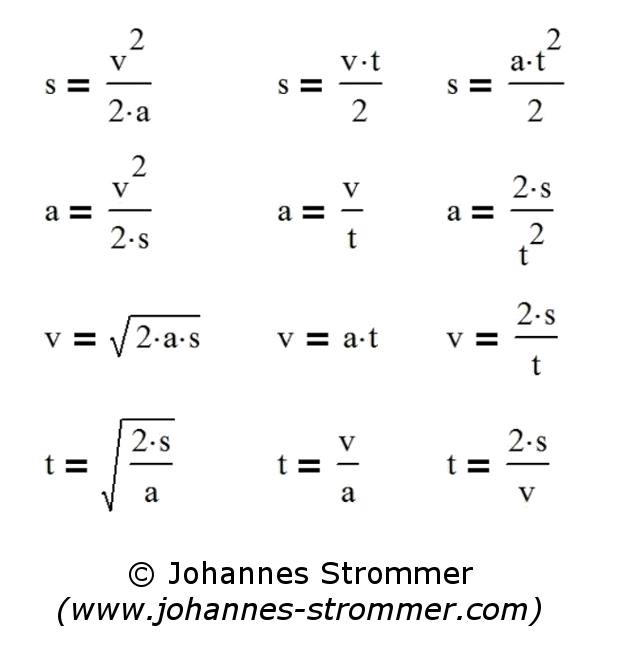
Meaning of the Variables
| v | final velocity in m/s |
| v0 | starting velocity in m/s |
| a |
acceleration or deceleration in m/s² |
| s | (braking) distance (= difference of ways) in m |
| t | time needed (= difference of times) in s |
Formuals for Uniform Acceleration – Starting Velocity ≠ 0
The following formulas apply to a uniform (= constant) acceleration or deceleration (= braking, negative acceleration) only with an initial velocity not equal to 0. Please note the hint on differences. For the meaning of the variables, see the previous table!

Example with starting distance s0
If there is a starting distance, s is replaced by s – s0 in the formula for the distance (1st line, 3rd column). Then move s0 to the other side to get the distance s you are looking for:
$$s=\frac{a}{2}·t^2+v_0·t\Rightarrow s-s_0=\frac{a}{2}·t^2+v_0·t\Rightarrow s=\frac{a}{2}·t^2+v_0·t+s_0$$
Simple Example
This example shows that the above formulas can also be easily used in practice. You only need a stopwatch, which is available on every smartphone, and a measuring tape.
Specification
A garden train leaves at 16:10:05 and reaches its top speed at 16:10:11. It covers a distance of 9 m. Assumed that the initial speed is 0 m / s (acceleration from standstill) and the acceleration is constant
- the time required
- the acceleration,
- the final velocity and
- the average speed has to be calculated.
Calculation of time
The time required for the acceleration process is the difference between the two times:
$$11 – 5 = 6 \Rightarrow t = 6\ s$$
Calculation of acceleration
If you insert in the formula of the 2nd line last column you get the acceleration you are looking for:
$$a = \frac{2⋅s}{t^2} = \frac{2⋅9\ m}{(6\ s)^2}\Rightarrow a = 0.5\ m/s^2$$
Calculation of the final velocity
Now you can easily calculate the speed by simply choosing one of the three formulas out of the 3rd line. If you use the 2nd formula you get:
$$v = a⋅t = 0.5\ m/s^2⋅6\ s \Rightarrow v = 3\ m/s$$
If you want to know the speed in km/h, multiply v by 3.6: 3⋅3.6 = 10.8 km/h
Calculation of the average speed
Since the distance is 0 at time t = 0 (= at the beginning) you only need to divide two numbers. Inserting in formula v = s/t results in:
$$v =\frac{9\ m}{6\ s} \Rightarrow v = 1.5\ m/s = 1.5⋅3.6\ km/h = 5.4\ km/h$$
As you can see, the average speed is only half the final velocity.
Current Velocity & Momentary Acceleration
If the acceleration is not constant, the use of the above formulas is not allowed. Instead, one calculates the acceleration, the velocity or the distance by differential or integral calculation.
Main Formulas
The current velocity v(t) at any time t is calculated by deriving the function of distance s(t) once from time t (= differential quotient):
$$v(t)=\frac{d}{dt}s(t)=\dot s(t)$$
If the momentary acceleration is known, the function of acceleration a(t) must be integrated after time t in order to get the current velocity v(t):
$$v(t)=\int a(t)dt$$
You get the momentary acceleration a(t) by deriving the function of speed v(t) once or by deriving the function of distance s(t) twice after time t:
$$a(t)=\frac{d}{dt}v(t)=\dot v(t)$$
$$a(t)=\frac{d^2}{d^2t}s(t)=\ddot s(t)$$
Distance s(t) is obtained by integrating the velocity v(t):
$$s(t)=\int v(t)dt$$
Meaning of the Variables
| v(t) |
Function of current speed |
| s(t) |
Function of distance |
| a(t) |
Function of momentary acceleration |
| t | time |
Page created on 31.03.2020. Last change: 29.11.2021.