Dieser Online-Rechner berechnet den Umfang, die Grundfläche, die Mantelfläche, die Oberfläche und das Volumen verschiedener Holz- oder Stahlprofile (= Prismen bzw. Träger). Diese Berechnungen können auch für Pyramiden und teilweise für Kugeln bzw. Kugelteile (Kugelsektor & Kugelsegment) und Tori durchgeführt werden.
Für die Berechnung von Gewicht, Masse und Streckenlast stehen als Werkstoff viele Metalle wie Stahl, Aluminium, Messing, Blei, Platin, Silber & Gold, unterschiedliche Holzarten sowie Beton und Fensterglas zur Auswahl. Nach dem Rechner finden sich Informationen zu verschiedenen Körpern sowie die Formeln zur Berechnung von Masse und Gewicht.
Link zu Unterseite:
Werbung
Rechner für Gewicht, Masse, Oberfläche & Volumen
Mit der Voreinstellung können Sie das Gewicht, die Masse, den Flächeninhalt der Grundfläche, den Umfang, die Mantelfläche, die Oberfläche und das Volumen für einen Quader (= spezielles Prisma) aus Stahl berechnen.
* Wird automatisch durch die Auswahl eines Werkstoffs eingetragen, kann jederzeit geändert werden.
** Um diese Werte eingeben zu können, wählt man unter Prisma/Drehzylinder –> Grundfläche –> Sonstige Profile –> „Eigenes Profil“. Es ist der Umfang der Grundfläche A gemeint.
Die Länge a steht immer normal (rechter Winkel = 90°) auf die Länge b!
Erklärung der Abkürzungen
| Dm | Durchmesser |
| Drehzyl. | Drehzylinder |
| Grundfl. | Grundfläche |
| Mantelfl. | Mantelfläche |
Formeln zur Berechnung von Masse und Gewicht
Mit den folgenden Formeln können die Masse und das Gewicht berechnet werden. Das Volumen und die Dichte müssen bekannt sein:
| Masse | m = ρ · V | Masse = Dichte mal Volumen |
| Gewicht | G = m · g | Gewicht = Masse mal Erdbeschleunigung |
Die Erdbschleunigung g wird auf der Erde mit 9.81 m/s² angenommen.
Link zu Unterseite:
Hinweise für die Verwendung des Rechners
- Folgende Querschnitte, die der Grundfläche eines Prismas entsprechen, sind verfügbar:
-
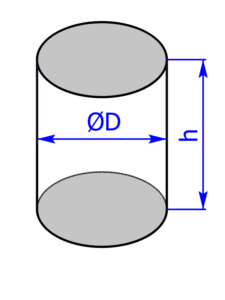
- Kreis (Rundstange = Drehzylinder)
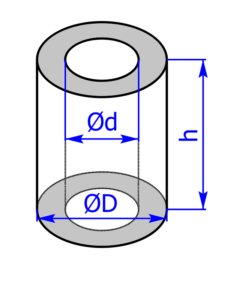
- Kreisring (Rundrohr = Hohlzylinder)
- Halbkreis (Halb-Rundstab)
- Rechteck-Profil (z . B. Flachstahl)
- Rechteck mit Bohrung
- Rechteck-Hohlprofil (Formrohr / Vierkantrohr)
- I-Träger bzw. H-Profil (= Doppel-T-Träger)
-
- U- bzw. C-Profil
- T-Profil
- L-Profil (Winkelprofil), gleich- & ungleichschenkelig
- Gleichschenkeliges und gleichseitiges Dreieck
- Regelmäßiges Sechseck/Sechskant
- Regelmäßiges Achteck/Achtkant
- Neben den oben angeführten Prismen können folgende Körper berechnet werden:
- regelmäßige dreiseitige, vierseitige (= quadratische), sechsseitige und achtseitige Pyramide
- Drehkegel
- Vollkugel, Hohlkugel (= Kugelschale), Kugelsegment und Kugelsektor
- Volltorus („Schwimmreifen“)
- Die Berechnung für das Volumen gilt auch für schiefe Pyramiden bzw. Prismen!
- Weiter unten findet man Skizzen von allen zur Auswahl stehenden Körpern.
- Für die richtige Funktion kann keine Gewähr übernommen werden – für Berichtigungen und Verbesserungsvorschläge bitte um Nachricht mittels Kontaktformular!
Begriffsklärung
Was versteht man unter Prisma, Kugelsegment, Kugelsektor und Torus?
Prisma
Als Prisma bezeichnet man einen Körper, dessen Grund- und Deckflächen kongruent (also deckungsgleich) und parallel zueinander sind. Alle Seitenflächen zusammen werden als Mantelfläche bezeichnet. Die Grundfläche kann aus beliebigen Vielecken bestehen.
Es gibt gerade und schiefe Prismen: Bei geraden Prismen stehen die Seitenflächen normal auf die Grundfläche.
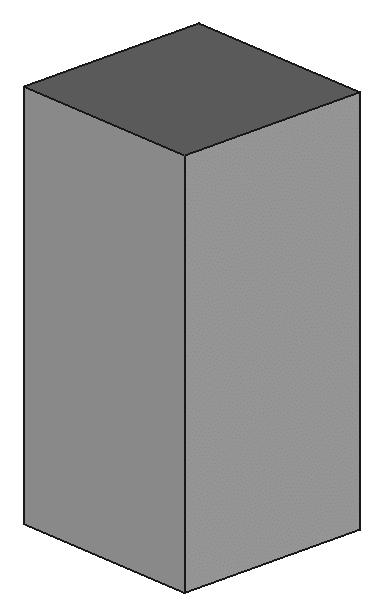
Ein besonderes Prisma ist der Quader, dessen sechs Flächen alle Rechtecke sind, siehe Abbildung. Der Würfel (auch regelmäßiges Hexaeder genannt) ist ein spezieller Quader: Bei diesem Körper sind die zwölf Seiten gleich lang und stehen auf einander normal, zudem sind alle sechs Flächen gleich groß.
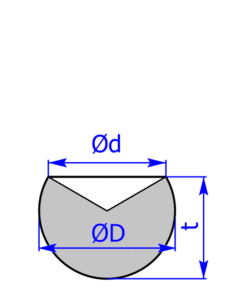
Kugelsegment oder Kugelabschnitt
Teilt man eine Vollkugel in zwei Teile, erhält man zwei sogenannte Kugelsegmente. Eine anderere Bezeichnung dafür ist Kugelabschnitt.
Die entstehende Schnittfläche ist eine Kreisfläche und bildet zusammen mit dem gekrümmten Teil, der Kugelkalotte oder auch Kugelhaube bzw. Kugelmütze genannt wird, die Oberfläche des Kugelsegments. Verläuft der Schnitt genau durch den Kugelmittelpunkt, erhält man zwei gleich große Körper, die Halbkugeln heißen.
Viele Kirchen besitzen Dächer in Kugelsegmentform, die als Kuppel oder Dom bezeichnet werden.

Kugelsektor oder Kugelausschnitt
Beim Kugelsektor – auch als Kugelausschnitt bezeichnet – gibt es drei Ausführungen, die vom Öffnungswinkels des drehkegelförmigen Ausschnitts abhängen. Die Spitze des Kegels liegt stets genau im Mittelpunkt der Kugel.
- Der Winkel beträgt weniger als 180° (Abbildung 1).
- Der Winkel beträgt genau 180°, es handelt sich also um eine Halbkugel.
- Der Winkel beträgt mehr als 180° (Abbildung 2).


In der Praxis ist dieser Körper kaum von Bedeutung.
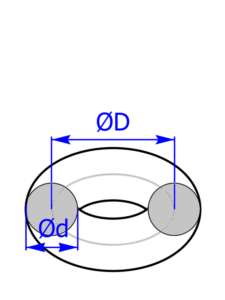
Torus und Volltorus
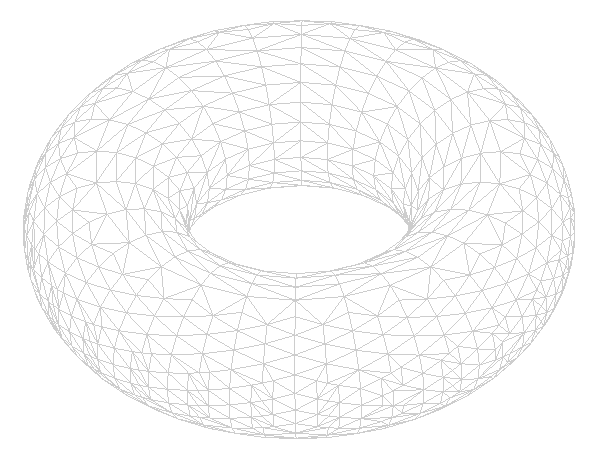
Rotiert eine Kreisfläche um eine Achse, die in der Kreisebene liegt, entsteht ein sogenannter Volltorus. Der Abstand vom Kreismittelpunkt zur Rotationsachse muss dabei größer als der Radius des Kreises sein, das heißt, die Achse darf die Kreisfläche nicht schneiden.
Lässt man dagegen nur den Umfang des Kreises um diese Achse rotieren, nennt man dieses Gebilde Torus.
Tori (= Mehrzahl von Torus) kennt jeder: ein Schwimmreifen ist mathematisch betrachtet ein Torus.
Skizzen der verfügbaren Körper
Skizzen der Prismen
Die folgenden 14 Profile können beim Rechner als Grundfläche ausgewählt werden:
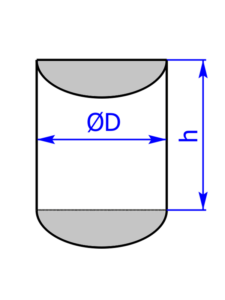
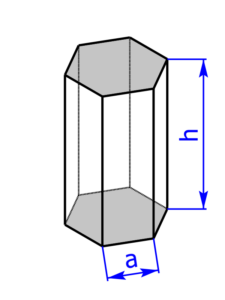
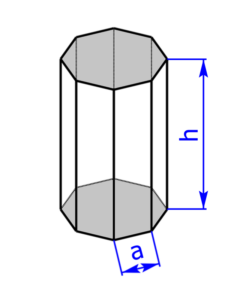
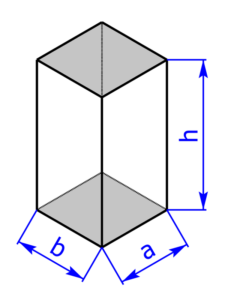
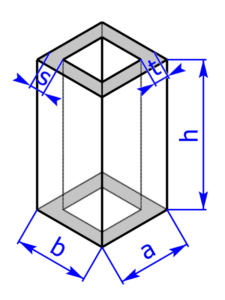
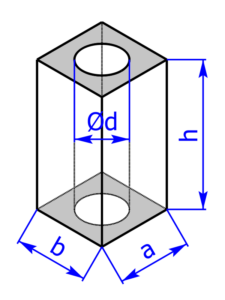
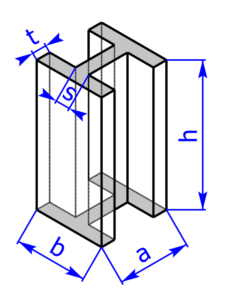
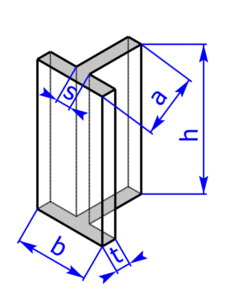
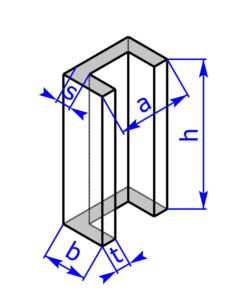
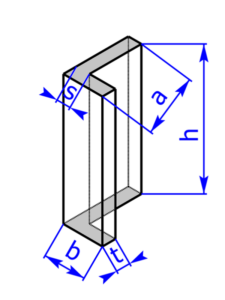
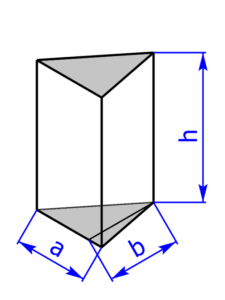
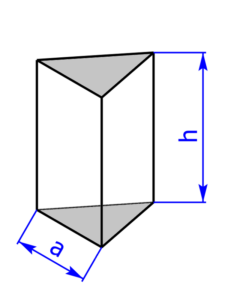
Skizzen der Pyramiden bzw. des Drehkegels
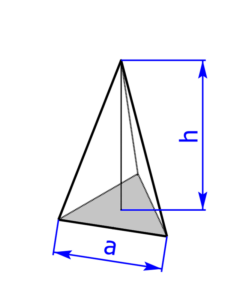
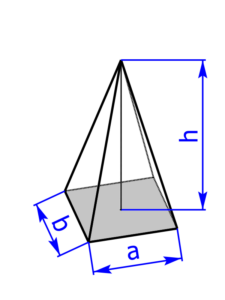
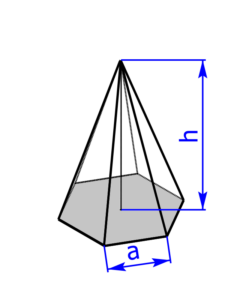
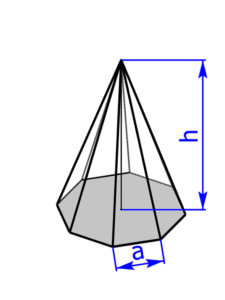
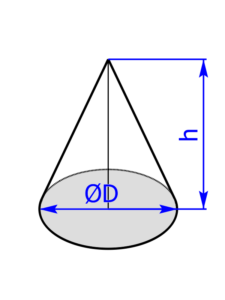
Skizzen der Kugeln bzw. des Torus
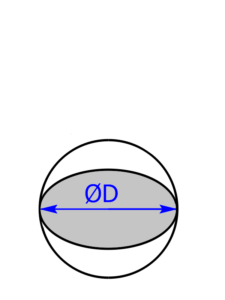
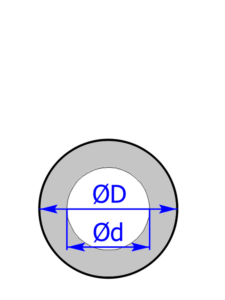
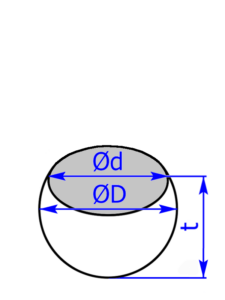
Werbung
Seite erstellt im Juni 2019. Zuletzt geändert am 29.07.2022.