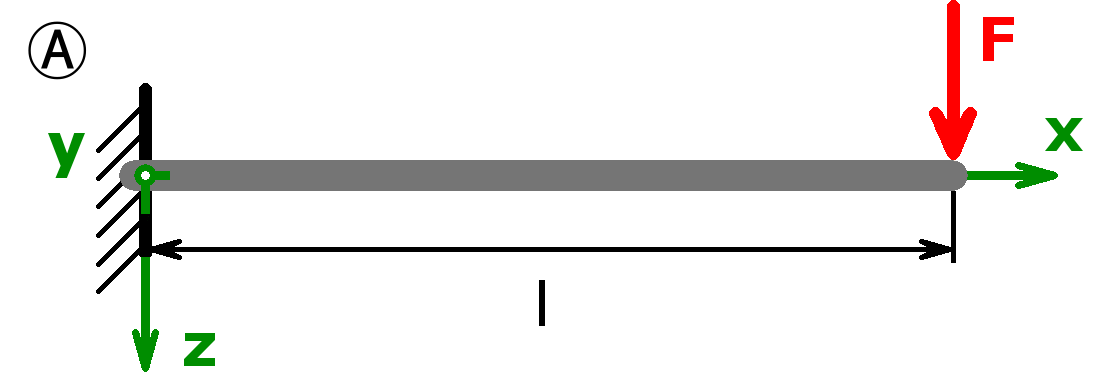Auf dieser Seite finden Sie zwei Tabellen mit den Formeln zur Berechnung der Auflagerkräfte und Einspannmomente (= Auflagerreaktionen), der Neigungswinkel und der (maximalen) Durchbiegung für einige wichtige Belastungsfälle sowohl für statisch bestimmte Systeme als auch für statisch unbestimmte Systeme. Natürlich werden auch die in den Formeln verwendeten Variablen erklärt.
Zudem gibt es hier Links zu Unterseiten, falls Sie an der Herleitung dieser Formeln Interesse haben. Sollten Sie hingegen nur etwas berechnen wollen, können Sie auch meinen Balkenrechner verwenden.
Links zu Unterseiten:
- Balkenrechner für statisch bestimmte und statisch unbestimmte Balken
- statisch bestimmte Träger: Lagerreaktionen berechnen
- statisch unbestimmter Träger: Satz von Menabrea
- Superpositionsprinzip – Überlagerung von Belastungen: Diese Methode kann bei nicht in dieser Formelsammlung angeführten Lastfällen angewendet werden.
Werbung
Formeln und Erklärung der Variablen
Die maximale Durchbiegung des Balkens kann mit den angegebenen Formeln in der Regel nur für eine Gleichlast oder für eine Dreieckslast berechnet werden. Eine Ausnahme stellt der statisch bestimmte Träger auf 2 Stützen dar, der mit der Einzelkraft F belastet wird: Für diesen Fall sind die Formeln zur Berechnung der maximalen Durchbiegung angeführt.
Im Falle einer Einzellast F wird mit den Formeln in der Tabelle die Durchbiegung (= Verschiebung) an der Stelle dieser Last F berechnet. Allerdings unterscheidet sich dieser Wert in der Regel nicht viel von der maximalen Durchbiegung. Eine Ausnahme bildet der Kragarm oder auch Kragträger: Hier wird die maximale Durchbiegung berechnet, da die maximale Durchbiegung in diesem Fall der Durchbiegung an der Stelle der Kraft entspricht.
Hinweise
- Wird die Formel für eine Auflagerkraft oder ein Einspannmoment nicht angegeben, ist diese Größe nicht vorhanden. Sie hat also den Wert null. Das gilt zum Beispiel für die Kräfte in x-Richtung oder für die Einspannmomente bei Fest- und Loslagern. Ähnliches trifft auf die Neigungswinkel zu: Bei einer festen Einspannung ist die Verdrehung immer null und daher wird sie in der Tabelle auch nicht angeführt.
- Achtung: Der Winkel kommt bei der Berechnung in Radiant und nicht in Grad heraus!
Erklärung der Variablen
Diese Abkürzungen werden in den folgenden beiden Tabellen verwendet:
| FA | Auflagerkraft im Lager A in z-Richtung in N |
| FB | Auflagerkraft im Lager B in z-Richtung in N |
| MA | Einspannmoment im Lager A |
| f | Durchbiegung des Balkens an der Stelle der Einzelkraft F in mm |
| fm | maximale Durchbiegung des Balkens in mm |
| αA | Neigungswinkel im Lager A in rad |
| αB | Neigungswinkel im Lager B in rad |
| F | Einzelkraft in N |
| q | Streckenlast in N/mm |
| l | Länge des Balkens in mm |
| Iy | Flächenträgheitsmoment in mm4 |
| E | E-Modul in N/mm², passende Werte findet man zum Beispiel auf Wikipedia |
Tabelle mit Formeln für statisch bestimmte Träger
Können die gesuchten Auflagerreaktionen – also die Auflagerkräfte und die Einspannmomente – nur mit Hilfe der Gleichgewichtsbedingungen ermittelt werden, spricht man von einem statisch bestimmten System. Dazu zählen der Einfeldträger (Balken mit je einem Festlager und einem Loslager an beiden Enden) und der Kragarm, wobei die Belastung beim Einfeldträger eine Gleichlast, eine Einzellast oder eine Dreieckslast sein darf. Für den Kragarm sind nur die Formeln bei einer Einzellast am Ende des Trägers angegeben.
| Belastungsfall des Balkens |
Auflagerkräfte & Einspannmoment |
(maximale) Durch- biegung & Winkel |
|
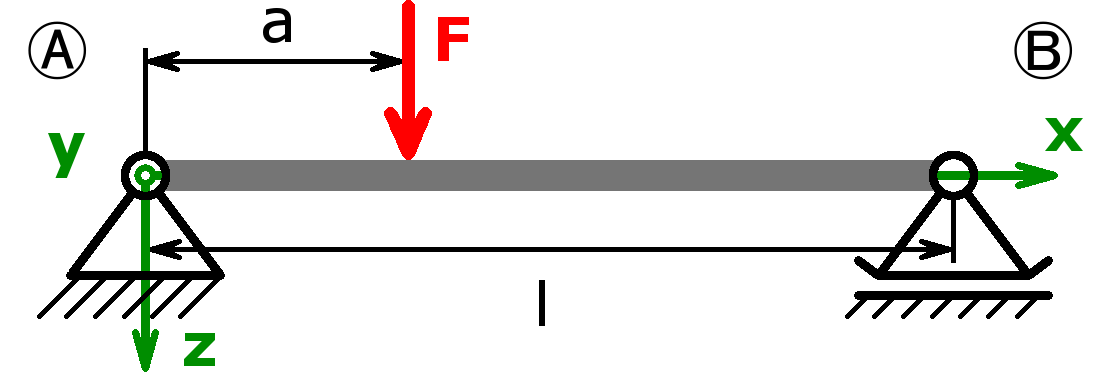
Festlager – Einzellast – Loslager (= Einfeldträger) |
$$F_A=F·\left(1-\frac{a}{l}\right)$$ $$F_B=\frac{F·a}{l}$$ |
Definition: b = l – a $$\alpha_A=\frac{F·a·b·(l+b)}{6·E·I_y·l}$$ $$\alpha_B=\frac{F·a·b·(l+a)}{6·E·I_y·l}$$ $$f=\frac{F·a^2·b^2}{3·E·I_y·l}$$ a > b: $$f_m =\frac{F·b\sqrt{(l^2-b^2)^3}}{9·\sqrt{3}·E·I_y·l}$$ a < b: $$f_m =\frac{F·a\sqrt{(l^2-a^2)^3}}{9·\sqrt{3}·E·I_y·l}$$ |
|
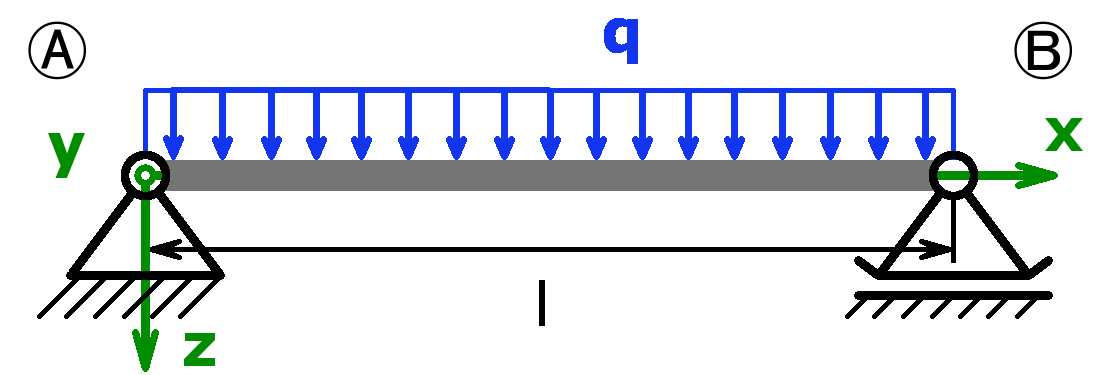
Festlager – Gleichlast – Loslager (= Einfeldträger) |
$$F_A=\frac{q·l}{2}$$ $$F_B=\frac{q·l}{2}$$ |
$$f_m=\frac{5·q·l^4}{384·E·I_y}$$ $$\alpha_A=\alpha_B=\frac{q·l^3}{24·E·I_y}$$ |
|
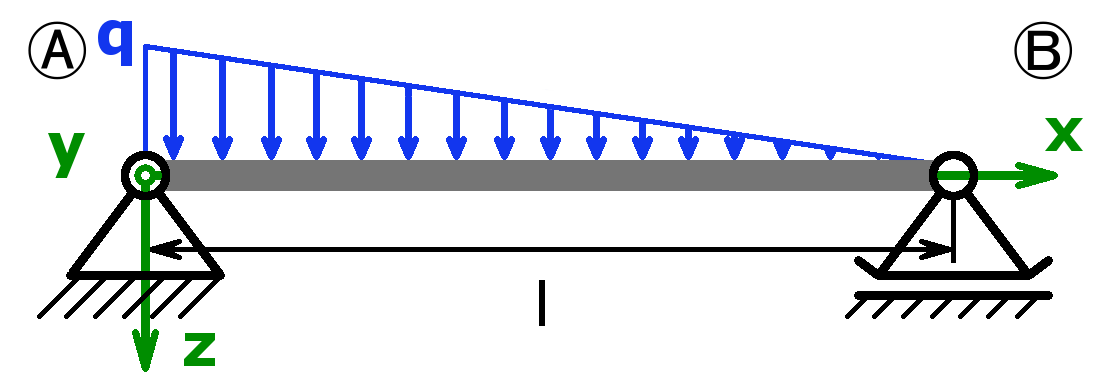
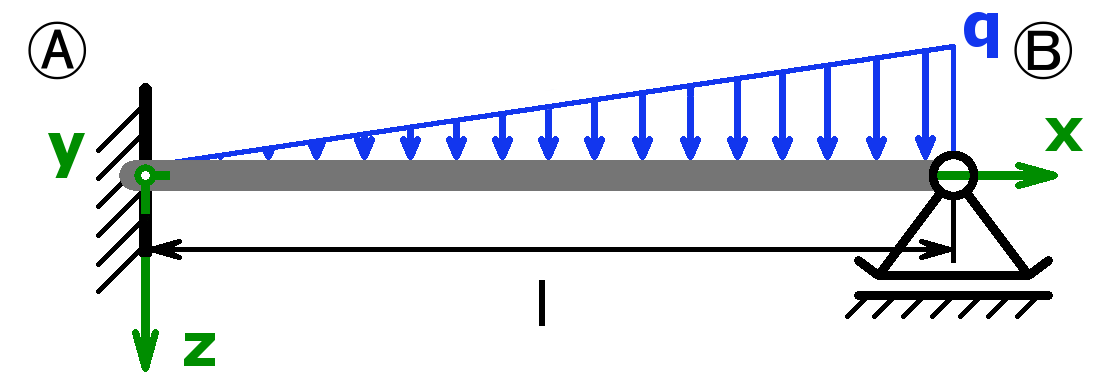
Festlager – Dreieckslast – Loslager |
$$F_A=\frac{q·l}{3}$$ $$F_B=\frac{q·l}{6}$$ |
$$f_m=\frac{q·l^4}{153,3·E·I_y}$$ $$\alpha_A=\frac{8·q·l^3}{360·E·I_y}$$ $$\alpha_B=\frac{7·q·l^3}{360·E·I_y}$$ |
|
Feste Einspannung – Einzellast – Freies Ende (= Kragträger/Kragarm) |
$$F_A=F$$ $$M_A=F·l$$ |
$$f=f_m=\frac{F·l^3}{3·E·I_y}$$ $$\alpha_B=\frac{F·l^2}{2·E·I_y}$$ |
|
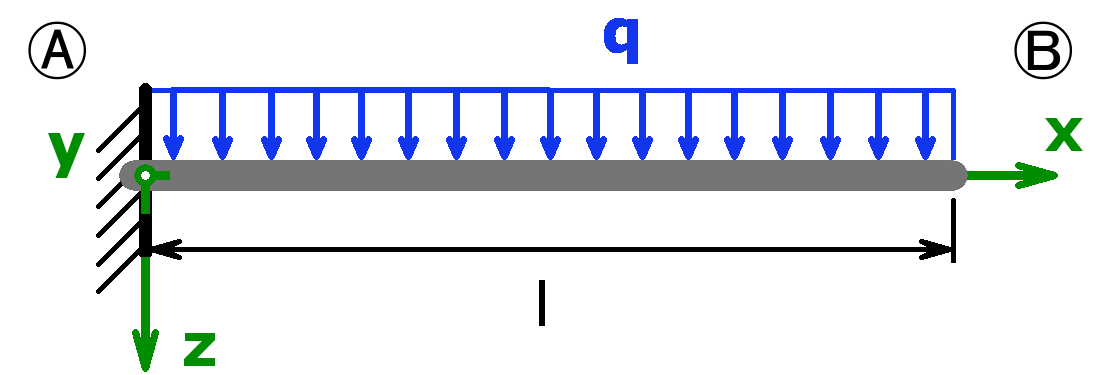
Feste Einspannung – Gleichlast – Freies Ende (= Kragträger/Kragarm) |
$$F_A=q·l$$ $$M_A=\frac{q·l^2}{2}$$ |
$$f_m=\frac{q·l^4}{8·E·I_y}$$ $$\alpha_B=\frac{q·l^3}{6·E·I_y}$$ >> Herleitung |
|
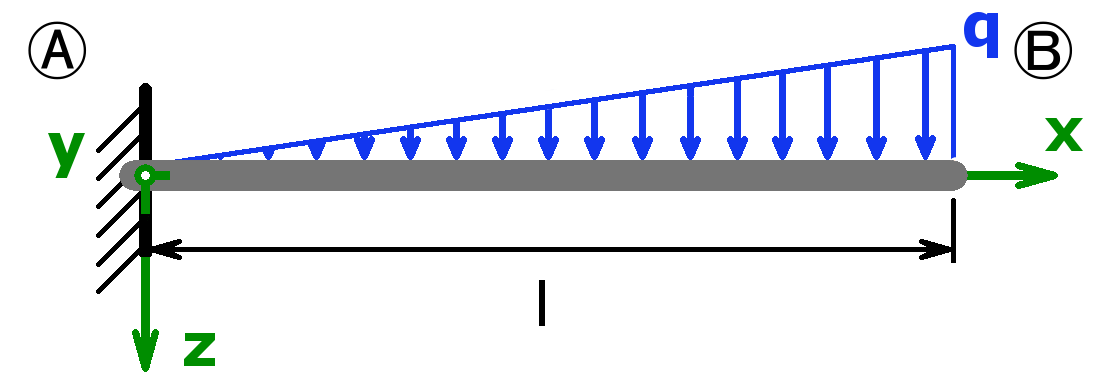
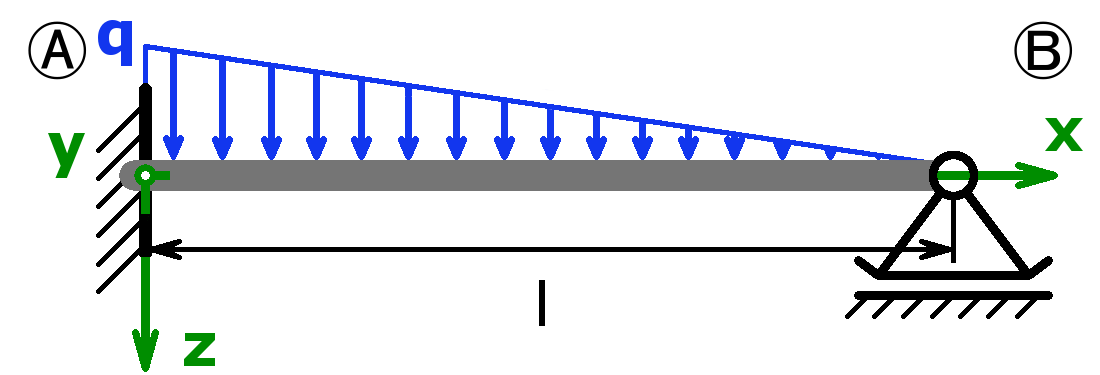
Feste Einspannung – Dreieckslast – Freies Ende |
$$F_A=\frac{q·l}{2}$$ $$M_A=\frac{q·l^2}{3}$$ |
$$f_m=\frac{11·q·l^4}{120·E·I_y}$$ $$\alpha_B=\frac{q·l^3}{8·E·I_y}$$ |
|
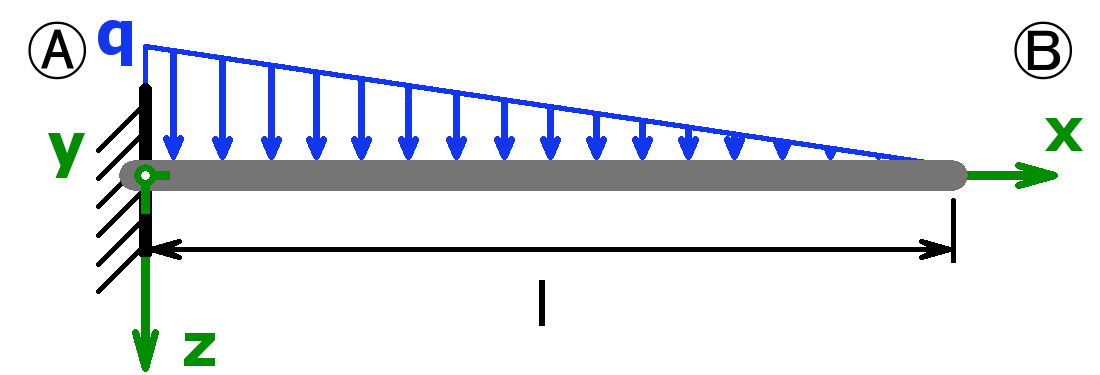
Feste Einspannung – Dreieckslast – Freies Ende |
$$F_A=\frac{q·l}{2}$$ $$M_A=\frac{q·l^2}{6}$$ |
$$f_m=\frac{q·l^4}{30·E·I_y}$$ $$\alpha_B=\frac{q·l^3}{24·E·I_y}$$ |
|
Festlager – Loslager – Einzellast (= Fliegende Lagerung) |
$$F_A=F·\left(\frac{l}{a}-1\right)$$ $$F_B=\frac{F·l}{a}$$ Anmerkung: FA wirkt hinunter, so wie F! |
$$f=\frac{F·(l-a)^2·l}{3·E·I_y}$$ $$\alpha_A=\frac{F·a·(l-a)}{6·E·I_y}$$ $$\alpha_B=\frac{F·a·(l-a)}{3·E·I_y}$$ |
Tabelle mit Formeln für statisch unbestimmte Träger
Bei statisch unbestimmten Systemen ist die Berechnung der Auflagerkräfte bzw. Einspannmomente nicht mehr so einfach. Man kann in diesem Fall zum Beispiel den Satz von Menabrea verwenden. Hier werden die Formeln für einen beidseitig eingespannten Träger angegeben und für einen Balken, der nur auf einer Seite eingespannt ist und auf der anderen Seite ein Festlager besitzt.
| Belastungsfall des Balkens |
Auflagerkräfte & Einspannmoment |
(maximale) Durch- biegung & Winkel |
|
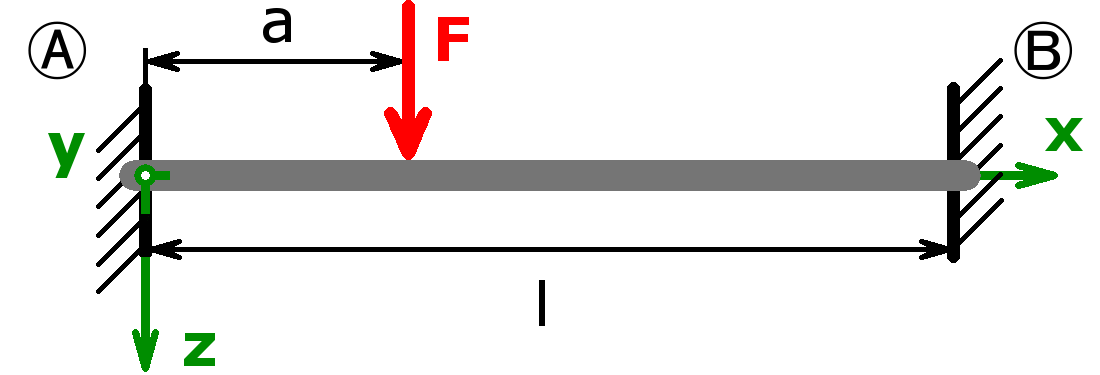
Feste Einspannung – Einzellast – Feste Einspannung |
$$F_A=F·\left(\frac{l-a}{l}\right)^2·\left(1+\frac{2·a}{l}\right)$$ $$F_B=F·\left(\frac{a}{l}\right)^2·\left(1+\frac{2·(l-a)}{l}\right)$$ $$M_A=-F·a·\left(\frac{l-a}{l}\right)^2$$ $$M_B=-F·(l-a)·\left(\frac{a}{l}\right)^2$$ $$f=\frac{F·a^3·(l-a)^3}{3·l^3·E·I_y}$$ |
|
|
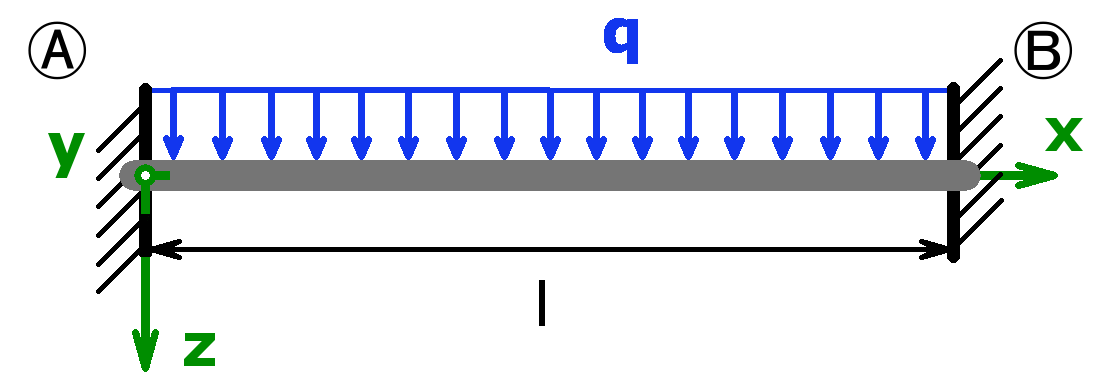
Feste Einspannung – Gleichlast – Feste Einspannung |
$$F_A=F_B=\frac{q·l}{2}$$ $$M_A=M_B=-\frac{q·l^2}{12}$$ >> Herleitung |
$$f_m=\frac{q·l^4}{384·E·I_y}$$ >> Herleitung |
|
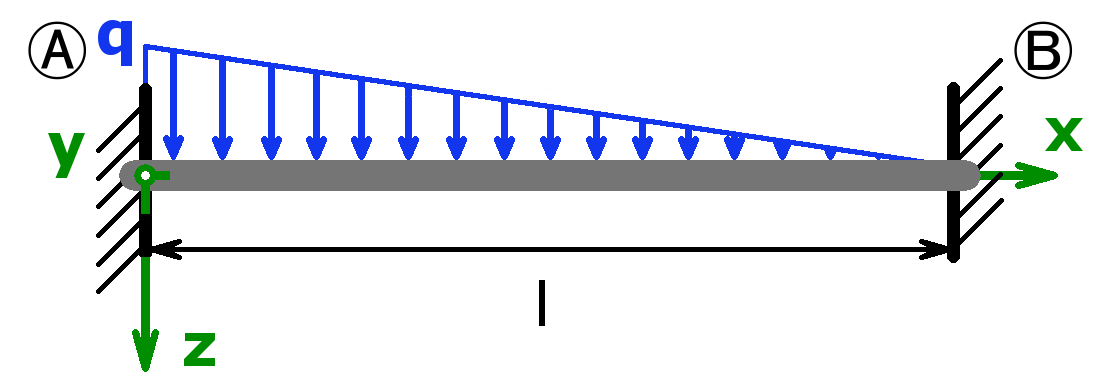
Feste Einspannung – Dreieckslast – Feste Einspannung |
$$F_A=\frac{7·q·l}{20}$$ $$F_B=\frac{3·q·l}{20}$$ $$M_A=-\frac{q·l^2}{20}$$ $$M_B=-\frac{q·l^2}{30}$$ |
$$f_m=\frac{q·l^4}{764·E·I_y}$$ |
|
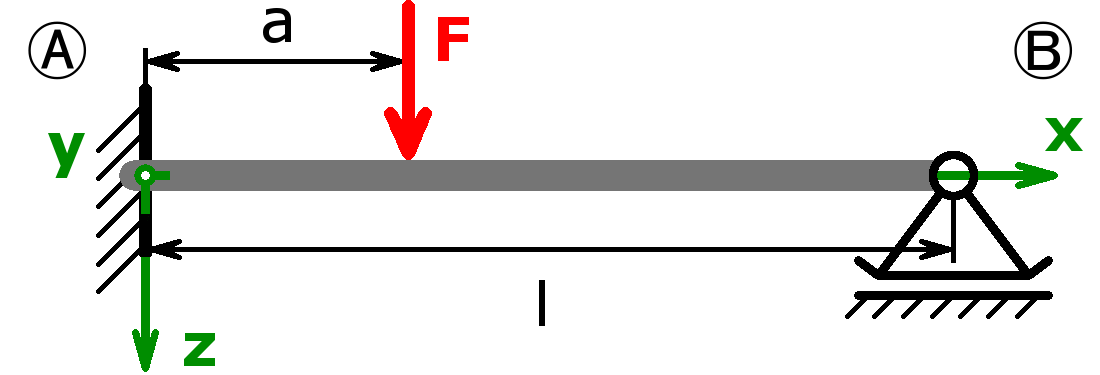
Feste Einspannung – Einzellast – Loslager |
$$F_A=F·\left(\frac{l-a}{l}\right)^2·\left(1+\frac{a}{2·l}+\frac{3·a}{2·(l-a)}\right)$$ $$F_B=F·\left(\frac{a}{l}\right)^2·\left(1+\frac{l-a}{2·l}\right)$$ $$M_A=\frac{F·a·(l-a)}{l}·\left(\frac{a}{2·l}-1\right)$$ $$f=\frac{F·(l-a)^2·a^3}{4·l^2·E·I_y}·\left(1+\frac{l-a}{3·l}\right)$$ $$\alpha_B=\frac{F·(l-a)·a^2}{4·l·E·I_y}$$ |
|
|
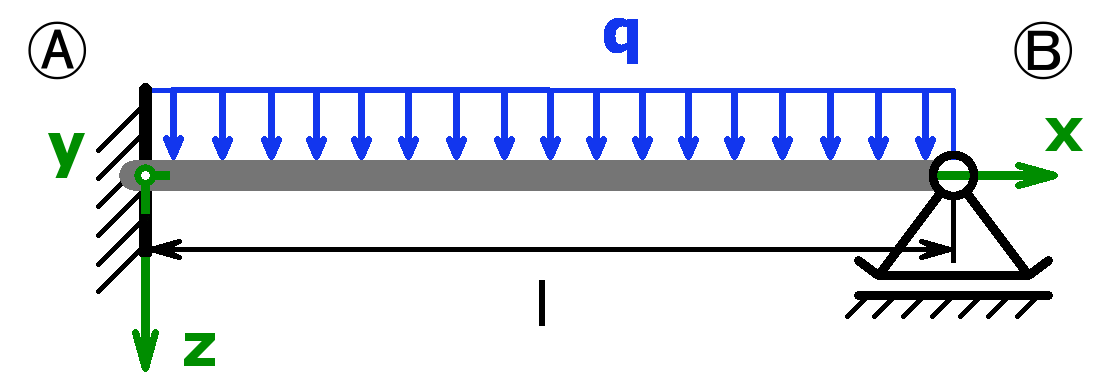
Feste Einspannung – Dreieckslast – Loslager |
$$F_A=\frac{5·q·l}{8}$$ $$F_B=\frac{3·q·l}{8}$$ $$M_A=-\frac{q·l^2}{8}$$ |
$$f_m=\frac{q·l^4}{185·E·I_y}$$ $$\alpha_B=\frac{q·l^3}{48·E·I_y}$$ |
|
Feste Einspannung – Dreieckslast – Loslager |
$$F_A=\frac{9·q·l}{40}$$ $$F_B=\frac{11·q·l}{40}$$ $$M_A=-\frac{7·q·l^2}{120}$$ |
$$f_m=\frac{q·l^4}{328·E·I_y}$$ $$\alpha_B=\frac{q·l^3}{80·E·I_y}$$ |
|
Feste Einspannung – Dreieckslast – Loslager |
$$F_A=\frac{4·q·l}{10}$$ $$F_B=\frac{q·l}{10}$$ $$M_A=-\frac{q·l^2}{15}$$ |
$$f_m=\frac{q·l^4}{419·E·I_y}$$ $$\alpha_B=\frac{q·l^3}{120·E·I_y}$$ |
Wie kommt man auf diese Formeln?
Hier finden Sie Links für die Herleitungen der Formeln:
- Bei der Berechnung der Auflagerreaktionen muss man zwischen statisch bestimmten und statisch unbestimmten Systemen unterscheiden:
- statisch bestimmte Träger: Lagerreaktionen berechnen
- statisch unbestimmter Träger: Satz von Menabrea
Werbung
Seite erstellt am 15.07.2020. Zuletzt geändert am 20.05.2022.