Auf dieser Seite findest du die Formeln zur Berechnung der Steigung bzw. des Gefälles von Straßen, Eisenbahnstrecken, Kanälen und dgl. Von einem Gefälle spricht man, wenn die Steigung negativ ist: Das ist der Fall, wenn man bergab fährt.
Zudem werden auch jene Formeln angegeben, die man benötigt, wenn man die Steigung von Prozent in Grad umrechnen möchte und umgekehrt.
Willst du nur die Steigung wissen und bist nicht an den Formeln interessiert? Dann ist mein Steigungsrechner ideal:
- Rechner für Steigungsberechnungen (auch Umrechnung zwischen Grad und Prozent)
- Die Steigungen von Tangenten werden mit der 1. Ableitung berechnet, siehe Seite Kurvendiskussion.
Inhaltsverzeichnis
Werbung
Skizze & Formeln zur Berechnung der Steigung
Hier sind die Formeln und eine dazu passende Skizze samt Erklärung der Abkürzungen zu finden.
Skizze
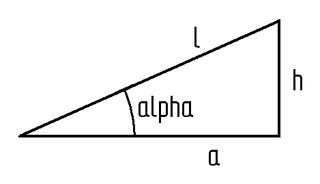
Erklärung der Abkürzungen
| a | horizontaler (= waagrechter) Abstand |
| h | Höhenunterschied (= vertikaler Abstand) |
| l | Länge der Schrägen, also z. B. die Länge der Straße |
| alpha | Steigungswinkel; Winkel zwischen Fahrbahn und Horizontalen |
Formeln
Die Steigung wird meist mit k oder m bezeichnet und ist definiert als Bruch:
$$k =\frac{h}{a}$$
Die Steigung wird also berechnet, indem man den Höhenunterschied durch die waagrechte Entfernung dividiert.
Mit den linken bzw. ersten beiden Formeln kann nun die Steigung in % bzw. in ‰ berechnet werden, wenn die waagrechte Entfernung a und der Höhenunterschied h bzw. die Steigung k bekannt sind:
Steigung in %
$$Steigung \nobreakspace in \nobreakspace \% =k⋅100 = \frac{h}{a}⋅100$$
Steigung in ‰
$$Steigung \nobreakspace in \nobreakspace ‰ =k⋅1000 = \frac{h}{a}⋅1000$$
Bis zu einer Steigung von ungefähr 10 % bzw. 5.7° kann man in guter Näherung statt der waagrechten Länge a auch die tatsächlich zurückgelegte, schräge Strecke l verwenden. Je kleiner die Steigung ist, desto geringer wird der Fehler.
Beispiel:
Bei einer Steigung von 10 % und einer waagrechten Entfernung von 100 m ist der tatsächlich zurückgelegte Weg nur um 0.5 m länger als die waagrechte Entfernung.
Berechnung der Länge l & Umformungen
Sind bei größeren Steigungen die Länge l und der horizontale Abstand a oder die Höhe h bekannt, wendet man zur Berechnung der Steigung zunächst den Satz des Pythagoras an. Dann formt man die Geleichung eventuell noch um und zieht anschließend die Wurzel, siehe nebenstehende Formeln. Hat man sich a bzw. h berechnet, kann anschließend die Steigung mit den obigen Formeln ermittelt werden.
$$l^2=a^2+h^2$$
$$l=\sqrt{a^2+h^2}$$
$$a=\sqrt{l^2-h^2}$$
$$h=\sqrt{l^2-a^2}$$
Angabe der Steigung als Verhältnis
Vor allem früher wurde die Steigung oftmals als Verhältnis 1:x angegeben:
$$k=\frac{1}{x}$$
Das bedeutet, dass man zum Beispiel für 1 Höhenmeter x Meter in waagrechter Richtung zurücklegen muss.
Es gilt also:
$$k=\frac{1}{x}=\frac{h}{a}$$
Man kann nun x durch Umformen der obigen Beziehung berechnen:
$$x=\frac{a}{h}=\frac{1}{k}$$
Beispiel: Steigung von 1:40
Das Verhältnis 1:40 kann man auch als Dezimalzahl bzw. in Prozent und Promille anschreiben:
$$k=\frac{1}{40}=0.025=2.5 \ \%=25 \ ‰$$
Winkelberechnung & Umrechnung von Prozent in Grad
Oft ist die Steigung in Grad gefragt bzw. ist der Steigungswinkel bekannt und die Steigung in Prozent gesucht. Zur Umrechnung zwischen diesen beiden Einheiten gibt es Formeln. Zudem wird nach diesen Formeln als Ergänzung eine Umrechnungstabelle von Prozent in Grad angegeben.
Formeln
Mit den folgenden Formeln erfolgt die Umrechnung von Prozent in Grad und umgekehrt:
$$\alpha=arctan(k)=arctan \left( \frac {h}{a}\right )$$
$$\alpha=arctan\left(\frac{Steigung\nobreakspace in \nobreakspace \%}{100}\right)$$
$$k=tan(\alpha)$$
$$Steigung\nobreakspace in \nobreakspace \%=tan(\alpha)⋅100$$
$$Steigung\nobreakspace in \nobreakspace ‰=tan(\alpha)⋅1000$$
Ähnlich geht man vor, wenn die Steigung in ‰ vorliegt: man nimmt einfach jeweils statt 100 die Zahl 1000. Der arctan entspricht auf den meisten Taschenrechnern der Taste tan-1.
Umrechnungstabelle von % in Grad
Grad ist die alltägliche Einheit für einen Winkel und wird mit dem Zeichen ° angeschrieben. Vor allem in der Technik ist auch die Einheit rad (= Radiant) sehr gebräuchlich.
Eine Steigung von 100 % ist entgegen der weit verbreiteten Meinung keine Senkrechte, sondern hat einen Winkel von “nur” 45 Grad. Für eine senkrechte Wand beträgt der Winkel 90°, während die Steigung in % unendlich ist. Zudem kann eine Steigung 100 % überschreiten. Allerdings werden Steigungen über 100 % fast immer in Grad angegeben.
Die nächste Tabelle zeigt, wie viel % Steigung einem Steigungswinkel in Grad entsprechen.
| Steigung in % | Winkel in Grad |
| 0 | 0 |
| 5 | 2.86 |
| 10 | 5.71 |
| 20 | 11.3 |
| 25 | 14.0 |
| 50 | 26.6 |
| 100 | 45 |
| 200 | 63.4 |
| 1000 | 84.3 |
| unendlich | 90 |
Werbung
Seite erstellt am 25.04.2021. Zuletzt geändert am 24.05.2022.