Hier finden Sie in einer Tabelle die Formeln zur Berechnung der Massenträgheitsmomente (kurz als Trägheitsmoment oder auch als Inertialmoment bezeichnet, früher Drehmasse) gängiger Körper:
- Vollzylinder
- Hohlzylinder
- Zylindermantel
- Quader
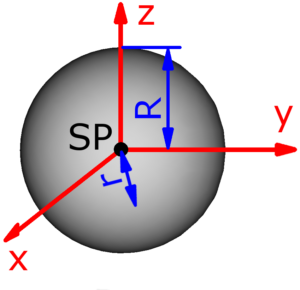
- Kugel
- Hohlkugel
- Kugelschale
- Punktmasse
- Vollkegel
- Kegelmantel
- Kegelstumpf
Zudem wird der Satz von Steiner angeführt und das Trägheitsmoment eines Hohlzylinders hergeleitet.
Links zu Unterseiten:
- Rechner für Massenträgheitsmomente
- Beispiel: Berechnung des Massenträgheitsmoments einer Riemenscheibe
Werbung
Tabelle mit Formeln von Massenträgheitsmomenten
Möchte man die Massenträgheitsmomente von dünnen Scheiben, dünnen Platten oder schlanken Stäben berechnen, können auch die unten stehenden Formeln verwendet werden – dazu muss nur die jeweilige Länge null gesetzt werden:
- dünne Scheibe: Formeln für Vollzylinder mit l = 0
- schlanker Stab: Formeln für Vollzylinder mit R = 0
- dünne Platte: Formeln für Quader mit a = 0, b = 0 oder h = 0
Die roten Pfeile stellen die Drehachsen dar, sie verlaufen – außer bei der Punktmasse – stets durch den Schwerpunkt des jeweiligen Körpers:
| Körper | Massenträgheits momente bezüglich der x-Achse |
Massenträgheits- momente bezüglich der y-Achse |
Massenträgheits- momente bezüglich der z-Achse |
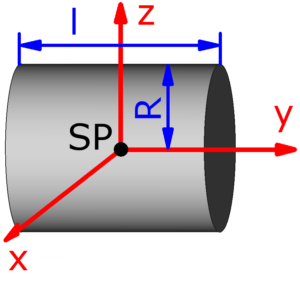 Vollzylinder |
$$J_x=\frac{m}{12}·(3·R^2+l^2)$$ | $$J_y=\frac{m·R^2}{2}$$ | $$J_z=\frac{m}{12}·(3·R^2+l^2)$$ |
 Zylindermantel |
$$J_x=\frac{m}{12}·(6·R^2+l^2)$$ | $$J_y=m·R^2$$ | $$J_z=\frac{m}{12}·(6·R^2+l^2)$$ |
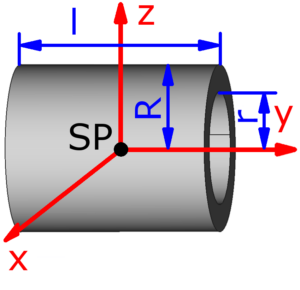 Hohlzylinder |
$$J_x=\frac{m}{12}·(3·(R^2+r^2)+l^2)$$ | $$J_y=\frac{m}{2}·(R^2+r^2)$$ | $$J_z=\frac{m}{12}·(3·(R^2+r^2)+l^2)$$ |
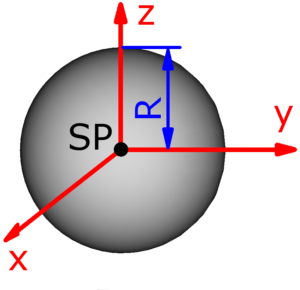 Vollkugel Vollkugel |
$$J_x=J_y=J_z=\frac{2·m·R^2}{5}$$ | ||
 Kugelschale Kugelschale |
$$J_x=J_y=J_z=\frac{2·m·R^2}{3}$$ | ||
|
|
$$J_x=J_y=J_z=\frac{2·m}{5}·\frac{R^5-r^5}{R^3-r^3}$$ | ||
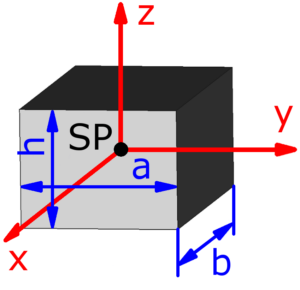 Quader Quader |
$$J_x=\frac{m}{12}·(a^2+h^2)$$ | $$J_y=\frac{m}{12}·(b^2+h^2)$$ | $$J_z=\frac{m}{12}·(a^2+b^2)$$ |
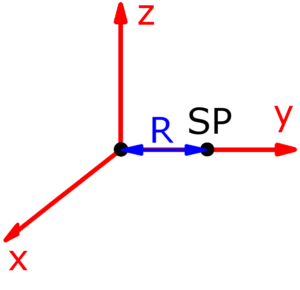 Punktmasse Punktmasse |
$$J_x=m·R^2$$ | $$J_y=0$$ | $$J_z=m·R^2$$ |
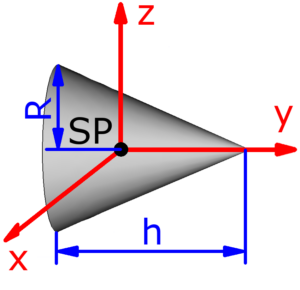 Vollkegel Vollkegel |
$$J_x=\frac{3·m}{20}·(R^2+4·h^2)$$ | $$J_y=\frac{3}{10}·m·R^2$$ | $$J_z=\frac{3·m}{20}·(R^2+4·h^2)$$ |
 Kegelmantel Kegelmantel |
$$J_y=\frac{m·R^2}{2}$$ | ||
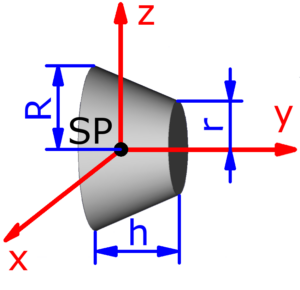 Kegelstumpf Kegelstumpf |
$$J_y=\frac{3·m}{10}·\frac{R^5-r^5}{R^3-r^3}$$ | ||
Besonderheiten
- Bei zylindrischen und kegeligen Körpern sind die Massenträgheitsmomente um zwei Achsen identisch. Beim vom Rechner verwendeten Koordinatensystem sind das die Trägheitsmomente bezüglich der x- und der z-Achse, da diese Körper rotationssymmetrisch um die y-Achse sind.
- Bei einer Kugel und bei einem Würfel sind sogar alle drei Massenträgheitsmomente gleich groß.
- Das Trägheitsmoment eines Kegelmantels entspricht dem Trägheitsmoment eines Vollzylinders (jeweils auf die y-Achse bezogen).
Zusammengesetzte Massenträgheitsmomente & Satz von Steiner
Einen komplexen Körper kann man meist aus mehreren einfachen Teilkörpern zusammensetzen. Die Massenträgheitsmomente von Teilkörpern kann man beliebig addieren bzw. auch subtrahieren, wenn sich deren Schwerpunkte (Massenmittelpunkte) auf derselben Achse befinden – siehe Herleitung der Formeln für einen Hohlzylinder im folgenden Abschnitt.
Liegen die Schwerpunkte von zwei Teilkörpern jedoch auf zu einander parallelen Achsen, wird das gesamte Massenträgheitsmoment JB bezüglich der betrachteten Achse mit dem Satz von Steiner berechnet:
$$J_B = J + m · d^2$$
Erklärung der Variablen:
| J |
Massenträgheitsmoment eines Teilkörpers bezüglich einer Achse durch dessen Schwerpunkt. Die Berechnung erfolgt mit den Formeln aus der oberen Tabelle. |
| m | Masse des Teilkörpers |
| d | Abstand zwischen den parallelen Drehachsen |
Rechenbeispiel – auch Anwendung des Satz von Steiner:
Herleitung der Formeln für einen Hohlzylinder
Ausgehend vom Trägheitsmoment eines Vollzylinders wird das Massenträgheitsmoment eines Hohlzylinders durch Abziehen der Trägheitsmomente von zwei Vollzylindern mit unterschiedlichen Radien berechnet.
Definitionen
Zunächst benötigen wir ein paar Definitionen:
Allgemeiner Vollzylinder
Trägheitsmoment um y-Achse:
$$J_y=\frac{m·R^2}{2}$$
Trägheitsmoment um x- bzw. z-Achse:
$$J_x=\frac{m}{12}·(3·R^2+l^2)$$
Masse:
$$m=\rho · V=R^2 · \pi · l · \rho$$
Äußerer Vollzylinder 1 mit dem Radius R und der Masse m1
Trägheitsmoment um y-Achse:
$$J_{y_1}=\frac{m_1·R^2}{2}$$
Trägheitsmoment um x- bzw. z-Achse:
$$J_{x_1}=\frac{m_1}{12} · (3 · R^2+l^2)$$
Masse:
$$m_1=R^2 · \pi · l · \rho$$
Innerer Vollzylinder 2 mit dem Radius r und der Masse m2
Trägheitsmoment um y-Achse:
$$J_{y_2}=\frac{m_2 · r^2}{2}$$
Trägheitsmoment um x- bzw. z-Achse:
$$J_{x_2}=\frac{m_2}{12} · (3 · r^2+l^2)$$
Masse:
$$m_2=r^2 · \pi · l · \rho$$
Herleitung des Massenträgheitsmoments bezüglich der y-Achse
Nun kann das gesamte Massenträgheitsmoment des Hohlzylinders bezüglich der y-Achse als Differenz angeschrieben werden:
$$J_y=J_{y_1}-J_{y_2}=\frac{m_1·R^2}{2}-\frac{m_2·r^2}{2}$$
Herausheben von 1/2 und einsetzen für die beiden Massen ergibt:
$$J_y=\frac{1}{2}·(R^2·\pi·l·\rho·R^2-r^2·\pi·l·\rho·r^2)$$
Nun hebt man wieder heraus, wendet eine der binomischen Formeln an und sortiert die Terme etwas um:
$$J_y=\frac{\pi·l·\rho}{2}·(R^4-r^4)=\pi·l·\rho·(R^2-r^2)·\frac{1}{2}·(R^2+r^2)$$
Beim Ausdruck π*l*ρ*(R2 – r2) handelt es sich um die Masse eines Hohlzylinders. Also lautet das gesuchte Massenträgheitsmoment des Hohlzylinders um die y-Achse:
$$J_y=\frac{m}{2}·(R^2+r^2)$$
Herleitung des Massenträgheitsmoments bezüglich der x- bzw. z-Achse
Nun schreibt man wieder das gesamte Massenträgheitsmoment des Hohlzylinders als Differenz an, wobei die Trägheitsmomente um die x-Achse und die z-Achse gleich groß sind:
$$J_x=J_z=J_{x_1}-J_{x_2}=\frac{m_1}{12}·(3·R^2+l^2)-\frac{m_2}{12}·(3·r^2+l^2)$$
Durch Herausheben von 1/12, Einsetzen für die Massen und Auflösen der Klammern bekommt man:
$$J_x=J_z=\frac{1}{12}·(R^2·\pi·l·\rho·3·R^2+R^2·\pi·l·\rho·l^2-r^2·\pi·l·\rho·3·r^2-r^2·\pi·l·\rho·l^2)$$
Herausheben ergibt:
$$J_x=J_z=\frac{1}{12}·\left[3·\pi·l·\rho·(R^4-r^4)+l^2·\pi·l·\rho·(R^2-r^2)\right]$$
Durch Anwenden einer der binomischen Formeln erhält man:
$$J_x=J_z=\frac{1}{12}·\left[3·\pi·l·\rho·(R^2-r^2)·(R^2+r^2)+l^2·\pi·l·\rho·(R^2-r^2)\right]$$
Nun hebt man den Ausdruck π*l*ρ*(R2 – r2) heraus:
$$J_x=J_z=\frac{1}{12}·\pi·l·\rho·(R^2-r^2)·\left[3·(R^2+r^2)+l^2\right]$$
Der vorhin herausgehobene Ausdruck ist die Masse des Hohlzylinders. Daher lautet die Formel für das Massenträgheitsmoment des Hohlzylinders um die x- bzw. z-Achse:
$$J_x=J_z=\frac{m}{12}·\left[3·(R^2+r^2)+l^2\right]$$
Werbung
Seite erstellt am 11.06.2019. Zuletzt geändert am 14.11.2021.