Mit diesem Online-Rechner kannst du die beiden klassischen Bewegungsaufgaben „Einholen“ und „Aufeinander zufahren“ schnell und einfach lösen. Die konstanten Geschwindigkeiten der Fahrzeuge, die Zeitdifferenz und im Falle des Entgegenfahrens auch die Entfernung zwischen den zwei Orten müssen bekannt sein. Die Wege der beiden Fahrzeuge und ihre jeweiligen Fahrzeiten werden berechnet.
Nach dem Rechner findest du ausführliche Erklärungen und zwei typische Anwendungsbeispiele.
Werbung
Rechner
Mit der Voreinstellung werden die Wege und Fahrzeiten von zwei Fahrzeugen berechnet, die einander entgegen fahren. Deren Geschwindigkeiten und die Entfernung zwischen den beiden Startpunkten sind bekannt.
Erklärung der Abkürzungen
| Δt | Die Zeitdifferenz Δt kann sowohl positiv als auch negativ sein. Ist die Zeitdifferenz positiv, fährt das 2. Fahrzeug später ab als das Fahrzeug 1. Ist dieser Wert negativ, fährt das Fahrzeug 2 früher los. Es ist zu beachten, dass im Falle des „Einholens“ eine Zeitdifferenz zwingend erforderlich ist! |
| s | Der Gesamtweg s, der der Entfernung zwischen den beiden Orten entspricht, wird nur beim „Aufeinander zufahren“ benötigt. Im Falle des „Einholens“ sind nämlich die drei Wege s, s1 und s2 gleich groß und werden berechnet. Mehr Infos gibt es im Anschluss! |
| v1, v2 | Durchschnittsgeschwindigkeit von Fahrzeug 1 bzw. Fahrzeug 2 |
| t1, t2 | Fahrzeit von Fahrzeug 1 bzw. Fahrzeug 2 |
| s1, s2 | Zurückgelegter Weg von Fahrzeug 1 bzw. Fahrzeug 2 |
Hintergrundwissen und Formeln
Es sind die beiden Fälle „Aufeinander zufahren“ und „Einholen“ zu unterscheiden. Mit T wird stets der Treffpunkt der beiden Fahrzeuge bezeichnet. A und B sind die jeweiligen Startpunkte.
Aufeinander zufahren
Fahren zwei Fahrzeuge aufeinander zu, ist der Gesamtweg s, also der Abstand zwischen den beiden verschiedenen Ausgangsorten A und B, gleich der Summe aus den Wegen s1 und s2 der Fahrzeuge:
$$s=s_1+s_2$$
Diesen Zusammenhang zwischen den Wegen zeigt auch die folgende Skizze:
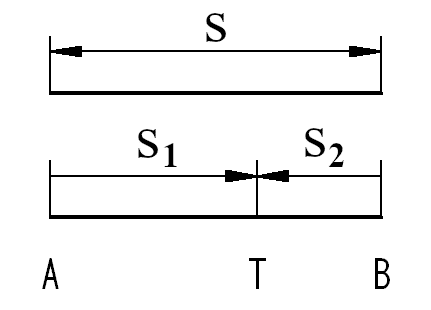
Beim „Aufeinander Zufahren“ muss der Gesamtweg s bekannt sein. Eine Zeitdifferenz Δt ist nicht unbedingt erforderlich. Das heißt, die Fahrzeuge können auch zur selben Zeit starten.
Einholen
In diesem Fall fahren beide Fahrzeuge vom selben Ort weg und holen einander nach einer gewissen Zeit ein. Die Wege s, s1 und s2 sind gleich groß, da die Fahrzeuge exakt dieselbe Strecke zurücklegen:
$$s=s_1=s_2$$
Auch dieser Zusammenhang wird in einer Skizze dargestellt:
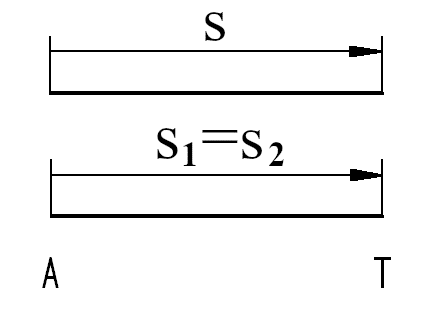
Es muss sowohl ein Geschwindigkeitsunterschied als auch eine Zeitdifferenz Δt vorliegen, da andernfalls kein Einholen möglich ist! Dafür wird der Gesamtweg s nicht benötigt.
Anwendungsbeispiele des Rechners
Hier findest du zwei typische Bewegungsaufgaben:
- Aufeinander zufahren von zwei Zügen
- PKW holt Radfahrer ein
Bewegungsaufgabe 1: Aufeinander zufahren von Zügen
Ein Railjet fährt mit einer mittleren Geschwindigkeit von 130 km/h um 9:30 von Linz Hbf. in Richtung St. Pölten Hbf. ab. Ein anderer Zug fährt 30 Minuten später von St. Pölten in Richtung Linz los. Die Durchschnittsgeschwindigkeit dieses Zuges beträgt 170 km/h. Die beiden Städte sind 130 km voneinander entfernt.
Wann treffen sich die beiden Züge? Wie weit ist diese Stelle von Linz bzw. von St. Pölten entfernt?
Lösung des Beispiels
Der 2. Zug fährt 30 Minuten später ab, also beträgt die Zeitdifferenz 0.5 Stunden: 30/60 = 0.5. Der Rechner ist daher für die Lösung dieser Aufgabe wie folgt auszufüllen:

Der erste Zug benötigt bis zum Treffpunkt 43 Minuten, daher begegnen sich die beiden Züge um 10:13. Anderer Lösungsweg: Der zweite Zug fährt 30 Minuten später ab, also um 10:00. Nach 13 Minuten Fahrzeit findet die Begegnung statt. Das ist um 10:13.
Der erste Zug fährt von Linz in Richtung St. Pölten und legt bis zum Treffpunkt 93.2 km zurück. Also ist der Ort der Begegnung 93.2 km von Linz entfernt. Der Weg s2 entspricht der Entfernung von St. Pölten.
Bewegungsaufgabe 2: PKW holt Radfahrer ein
Ein Radfahrer fährt mit einer mittleren Geschwindigkeit von 20 km/h um 12:00 von Salzburg in Richtung Bischofshofen los. 40 Minuten später folgt ihm ein Autofahrer mit einer Geschwindigkeit von 80 km/h.
Wann überholt der PKW den Radfahrer? Wie weit ist diese Stelle von Salzburg entfernt?
Lösung des Beispiels
Der PKW fährt 40 Minuten später ab, also beträgt die Zeitdifferenz 0.667 Stunden: 40/60 = 0.667. Der Rechner ist für die Lösung dieses Beispiels auf folgende Weise auszufüllen:
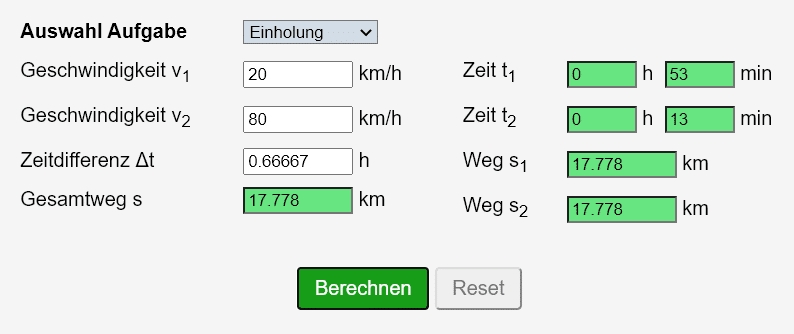
Nach 17.8 Kilometern überholt der Autofahrer den Radfahrer. Das ist um 12:53.
Werbung
Seite erstellt am 01.04.2021. Zuletzt geändert am 28.10.2021.